Archive for August 2015

KD 1,3 MEMAHAMI RELASI DAN FUNGSI

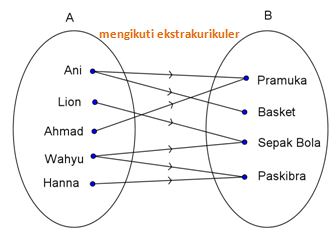
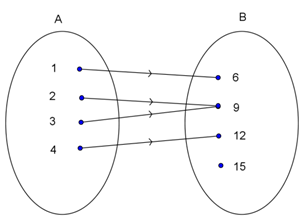
Pengertian Fungsi atau Pemetaan Fungsi (pemetaan) dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota him...

Cara Menyajikan Suatu Relasi Cara menyajikan suatu relasi adalah dengan diagram panah, diagram kartesius, dan himpunan pasangan berurut...

Pengertian Relasi Kata relasi tentu pernah kita dengar dalam kehidupan sehari-hari. Relasi berarti hubungan. Relasi dibentuk dari anggot...

Coba-coba soal kesebangunan....

Pada kesempatan ini menshare teknik mengatasi stress yang saya peroleh dari seminar yang saya ikuti.. semoga bermanfaat

Berikut foto-foto momen saat mengikuti lomba Lintas Graph Matematika (LGM) 2014 di FKIP UNTAN Pontianak. LIMAS 2014

Quipper school merupakan E-Learning yang cerdas, mudah dan kreatif Belajar kapan saja, dimana saja . Di kelas, di rumah, atau bahkan di ...

KD 1,2 Menguraikan bentuk aljabar kedalam faktor-faktornya Silahkan simak video dari youtube berikut untuk membantu pemahaman tentang pemfa...

KD 1.1 Melakukan operasi pada bentuk aljabar. Pengertian Koefisien, Variabel, Konstanta, Dan Suku 1. Variabel Variabel adalah lambang...

KD 1.2 Mengidentifikasi bangun segitiga yang sebangun dan kongruen Segitiga yang sebangun Pada KD 1.1 kita telah mempelajari syarat dua b...

KESEBANGUNAN KD.1.1 Mengidentifikasi bangun-bangun datar yang sebangun dan kongruen. SEBANGUN Dua buah bangun datar dikatakan sebangu...