KD 1.6 KONSEP GRADIEN

Pengertian Gradien

Perhatikan ilustrasi di bawah ini.

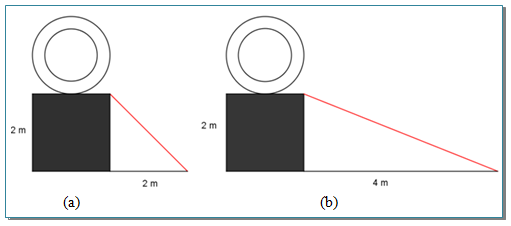
       Sebuah drum minyak telah berhasil dinaikkan dari lantai ke atas sebuah kontainer dengan bantuan papan (berwarna merah) dengan cara digelindingkan. Menurut pendapatmu, drum minyak mana yang lebih mudah dinaikkan ke atas kontainer? Menurut ilmu Fisika, kondisi mana yang lebih menghemat energi untuk memindahkannya? Ya, benar sekali. Kondisi (b) lebih menghemat energi karena kemiringan papan tidak terlalu menanjak ke atas.

       Andaikan papan (berwarna merah) dianggap sebagai suatu garis lurus, maka nilai kemiringan papan dalam matematika disebut dengan gradien (m). Selanjutnya, perhatikan kembali kondisi (a) dan (b). Apa yang membedakan keduanya? Perbedaannya terletak pada jarak ujung papan yang menyentuh lantai ke kontainer. Pada kondisi (a), jarak ujung papan yang menyentuh laintai ke kontainer adalah 2 meter, sedangkan pada kondisi (b) jaraknya 4 meter. Hal inilah yang menyebabkan perbedaan kemiringan di antara kedua papan.

Bagaimana dengan kondisi di bawah ini? Apakah nilai kemiringannya sama?

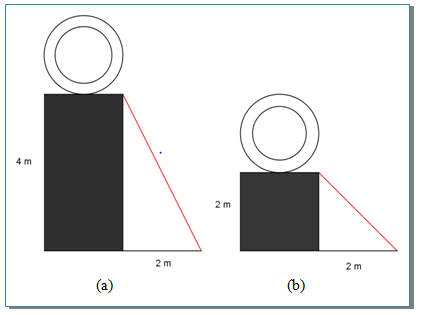
Dari gambar di atas, papan (a) dengan tinggi kontainer 4 meter, lebih miring dari papan (b). Berdasarkan dua ilustrasi yang telah disajikan, diperoleh:

Apabila bagian (b) dari gambar di atas digambarkan dalam koordinat kartesius dengan papan sebagai sebuah garis, maka akan diperoleh gambar berikut.

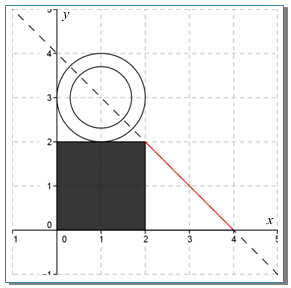
Dari gambar, kemiringan (gradien) garis dapat dirumuskan sebagai:

Perhatikan bahwa koordinat ujung-ujung papan adalah (4, 0) dan (2, 2), sehingga diperoleh:

(4, 0) → x1 = 4 dan y1 = 0
(2, 2) → x2 = 2 dan y2 = 2

Gradien atau kemiringannya adalah:

m=y2–y1x2–x1=2–02–4=2−2=−1

Jadi, kemiringan papan adalah -1.

Selanjutnya, kita akan menentukan:

• gradien dari garis yang melalui titik 2 titik yaitu (x1, y1) dan (x2, y2)
• gradien dari garis y = mx dan y = mx + c
• gradien dari garis ax + by = c atau ax + by + c = 0

Gradien Garis yang Melalui Titik (x1, y1) dan (x2, y2)

Seperti yang telah dijelaskan pada uraian sebelumnya, gradien (m) garis yang melalui 2 titikyaitu (x1, y1) dan (x2, y2) adalah:

m=y2–y1x2–x1

Contoh 1

Gradien garis yang melalui titik (3, -1) dan (1, 5) adalah ....

Penyelesaian:

Diketahui garis melalui titik (3, -1) dan (1, 5).

Ini berarti:
(3, -1) → x1 = 3 dan y1 = -1
(1, 5) → x2 = 1 dan y2 = 5

m=y2–y1x2–x1=5–(−1)1–3=6−2=−3
.
Jadi, gradiennya (m) = -3.

Gradien Garis y = mx dan y = mx + c

Dari penjelasan sebelumnya diperoleh bahwa:

Oleh karena persamaan garis y = mx melalui (0, 0) dan (x, y), maka berlaku m=yx. Hal yang sama juga berlaku pada persamaan garis y = mx + c. Jadi, gradien persamaan garis y = mxdan y = mx + c adalah nilai m atau koefisien variabel x.

Contoh 2

Tentukan gradien dari persamaan garis y = 3x.

Penyelesaian:

Persamaan garis y = 3x berbentuk y = mx, sehingga gradiennya merupakan koefisien dari variabel x yaitu 3.

Jadi, gradien dari y = 3x adalah 3.

Contoh 3

Tentukan gradiean dari persamaan garis y = -2x + 12.

Penyelesaian:

Persamaan garis y = -2x + 12 berbentuk y = mx + c, sehingga gradiennya merupakan koefisien dari variabel x yaitu -2.

Jadi, gradien dari y = -2x + 12 adalah -2.

Gradien Garis ax + by = c atau ax + by + c = 0

Untuk menentukan gradien dari persamaan garis ax + by = c, kita ubah bentuk persamaan tersebut ke dalam bentuk y = mx + c yaitu:

ax+by=c⇔by=−ax+c⇔y=−abx+cb

Oleh karena gradien persamaan y = mx + c adalah m atau koefisien variabel x, maka gradien persamaan y=−abx+cb adalah m=−ab.

Jadi, gradien garis ax + by = c atau ax + by + c = 0 adalah: 
m=−ab

Contoh 4

Gradien persamaan garis 3y + 2x = 12 adalah ...

Penyelesaian:

Persamaan garis 3y + 2x = 12 merupakan bentuk ax + by = c.

Ini berarti:
a = koefisien x = 2
b = koefisien y = 3

Jadi, gradien dari 3y + 2x = 12 adalah:
m=−ab=−23

Contoh 4 ini juga dapat diselesaikan dengan cara alternatif.

Cara Alternatif

Persamaan garis 3y + 2x = 12 merupakan bentuk ax + by = c.

Ubah 3y + 2x = 12 ke bentuk y = mx + c.
3y+2x=12⇔3y=−2x+12⇔y=−23x+123

Gradien dari y=−23x+123 adalah koefisien dari variabel x yaitu −23.

Jadi, gradien dari 3y + 2x = 12 adalah −23.

Perlu diingat bahwa tanda (+) atau (-) pada gradien menentukan arah kemiringan garis. Jika diperoleh gradien bernilai positif berarti arah garis naik dari kiri ke kanan, sedangkan gradien bernilai negatif berarti arah garis turun dari kiri ke kanan.