PELUANG (SMP)

PELUANG

Sebelum mempelajari topik ini, mari kita mengingat kembali tentang ruang sampel dan titik sampel.

             

Banyaknya titik sampel pada suatu kejadian dibandingkan dengan banyaknya ruang sampel inilah yang disebut dengan peluang. Misalkan K adalah suatu kejadian, maka peluang kejadian K dapat ditentukan dengan:

P(K)=n(K)n(S)

Keterangan:

P(K) = peluang kejadian K

n(K)= banyaknya titik sampel kejadian K

n(S)= banyaknya anggota ruang sampel kejadian K

Banyaknya titik sampel munculnya suatu kejadian tidak mungkin lebih dari banyaknya ruang sampel, sehingga nilai peluang terletak dari 0 sampai 1 atau 0 ≤ P(K) ≤ 1.

Jika suatu kejadian memiliki peluang 0, maka kejadian tersebut tidak mungkin terjadi, atau disebut dengan kejadian mustahil.

Jika suatu kejadian memiliki peluang 1, maka kejadian tersebut pasti akan terjadi atau disebut dengan kepastian atau kejadian mutlak.

PELUANG KOMPLEMEN SUATU KEJADIAN

Komplemen suatu kejadian merupakan himpunan kejadian yang mungkin terjadi selain kejadian tersebut. Misalkan terdapat suatu kejadian K, maka komplemen kejadian K adalah kejadian bukan K, ditulis dengan K’ (dibaca: K komplemen). Contoh kejadian komplemen ini dapat kalian jumpai pada pelemparan sebuah dadu. Komplemen kejadian munculnya angka 2 adalah munculnya angka 1, 3, 4, 5, dan 6. Contoh lain dapat kalian jumpai pada komplemen kejadian hari ini hujan adalah kejadian hari ini tidak hujan.

Hubungan peluang kejadian K dan kejadian bukan K ditentukan oleh rumus berikut.

P(K) + P(K’) = 1

P(K’) = 1 – P(K)

P(K) = 1 – P(K’)

Contoh 1

Sebuah dadu dilemparkan satu kali. Peluang munculnya mata dadu bilangan prima dan peluang munculnya mata dadu bukan bilangan prima adalah ....

Jawab:

Diketahui :

Ruang sampel pelemparan sebuah buah dadu adalah {1, 2, 3, 4, 5, 6}, sehingga n(S) = 6.

Misalkan K adalah kejadian munculnya mata dadu bilangan prima, maka titik sampel K adalah 2, 3, dan 5, sehingga n(K) = 3.

Dengan demikian, diperoleh peluang kejadian K adalah:

P(K)=n(K)n(S)=36=12

Ini berarti, peluang munculnya mata dadu prima adalah 12.

Peluang munculnya mata dadu bukan bilangan prima merupakan peluang komplemen dari peluang munculnya mata dadu prima. Dengan demikian, berlaku:

P(K’) = 1 - P(K)

          = 1 - 12

          = 12

Jadi, peluang munculnya mata dadu bilangan prima dan peluang munculnya mata dadu bukan bilangan prima adalah 12 dan 12.

Contoh 2

Tiga keping uang logam dilemparkan bersama. Peluang munculnya dua sisi koin menunjukkan angka adalah ....

Jawab:

Mula-mula, kita tentukan ruang sampel pelemparan tiga keping uang logam dengan menggunakan diagram pohon. Misalkan sisi gambar (G) dan sisi angka (A), maka:

                           

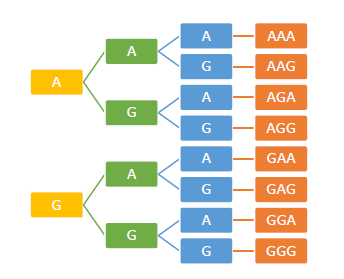
Ruang sampel : S = {(A, A, A), (A, A, G), (A, G, A), (A, G, G), (G, A, A), (G, A, G), (G, G, A), (G, G, A)}, sehingga n (S) = 8.

Misalkan K adalah kejadian munculnya dua sisi koin menunjukkan angka. Dari diagram pohon di atas, titik sampel munculnya kejadian K adalah {(AAG), (AGA), (GAA)}, sehingga n (K) = 3.

Jadi, peluang munculnya dua sisi koin menunjukkan angka adalah:

P(K)=n(K)n(S)=38

Contoh 3

Peluang esok hari turun hujan adalah 0,45. Peluang esok hari tidak turun hujan adalah ....

Jawab:

Misalkan A adalah kejadian esok hari esok hari turun hujan.

Diketahui peluang esok hari turun hujan adalah 0,45, maka P(A) = 0,45.

Misalkan A’ adalah kejadian esok hari tidak hujan, maka A’ adalah komplemen kejadian A. Dengan demikian, berlaku:

P(A’) = 1 - P(A)

⇔P(A’) = 1 - 0,45

⇔P(A’) = 0,55

Jadi, peluang esok hari tidak turun hujan adalah 0,55.