PENGERTIAN KUADRAN DALAM TRIGONOMETRI (SMA)

PENGERTIAN KUADRAN DALAM PERBANDINGAN TRIGONOMETRI

Gambar berikut memberikan ilustrasi tentang pembagian sudut dalam 4 kelompok kuadran.

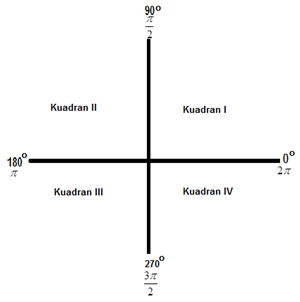
Misalkan besar sudut adalah α.

1. Jika 0° < α < 90° atau 0 < α < π2, maka α terletak di kuadran I.
2. Jika 90° < α < 180° atau π2 < α < π, maka α terletak di kuadran II.
3. Jika 180° < α < 270° atau π<α<32π, maka α terletak di kuadran III.
4. Jika 270° < α < 360° atau 32π < α < 2π, maka α terletak di kuadran IV.

Nah, bagaimanakah perbandingan sudut dalam masing-masing kuadran?

Sudut yang Terletak pada Kuadran I

Materi ini telah banyak kalian pelajari dalam materi tentang perbandingan trigonometri pada segitiga siku-siku. Apakah kalian masih ingat?

Berdasarkan gambar di atas, nilai perbandingan trigonometri pada kuadran I adalah sebagai berikut:

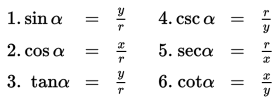
Jika kita perhatikan, ternyata semua nilai perbandingan trigonometri pada kuadran I bertanda positif (+).

Sudut yang Terletak pada Kuadran II

Letak sudut dalam kuadran II ditunjukkan dalam gambar berikut.

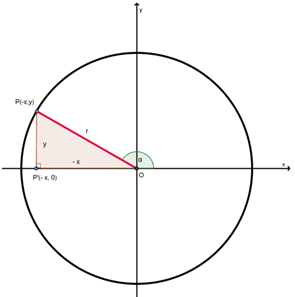
Bagaimanakah nilai perbandingan trigonometri pada kuadran II?
Bagaimana pula tanda dari setiap nilai perbandingan trigonometri tersebut?

Berikut ini adalah jawaban dari kedua pertanyaan di atas:

Sudut yang Terletak pada Kuadran III

Letak sudut α di kuadran III ditunjukkan oleh gambar berikut:

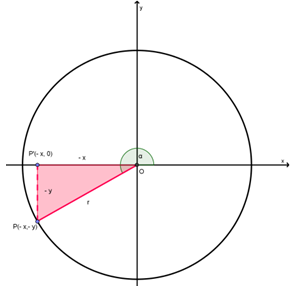
Berdasarkan gambar di atas, nilai perbandingan trigonometri pada Kuadran III adalah sebagai berikut:

Sudut yang Terletak pada Kuadran IV

Gambar berikut ini menunjukkan letak sudut α di kuadran IV.

Berdasarkan gambar di atas, nilai perbandingan trigonometri pada Kuadran IV adalah sebagai berikut:

Apa yang dapat kalian simpulkan mengenai penjelasan tentang tanda nilai perbandingan trigonometri dalam keempat kuadran?
Ilustrasi berikut ini menjelaskan kesimpulan dari penjelasan di atas.

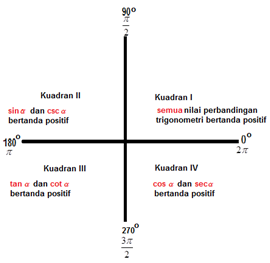
Sekarang kalian sudah mulai paham bukan?
Nah, untuk menambah pemahaman kalian, mari kita cermati beberapa contoh berikut.

Contoh 1:

Tentukan tanda dari setiap perbandingan trigonometri berikut:

1. sin 145°
2. cos 230°
3. tan 110°

Penyelesaian:

1. Oleh karena 90° < 145° < 180°, maka sudut 145° terletak di kuadran II → sin 145°bertanda positif.
2. Oleh karena 180° < 230° < 270°, maka sudut 230° terletak di kuadran III → cos 230°bertanda negatif.
3. Oleh karena 90° < 110° < 180°, maka sudut 110° terletak di kuadran II → tan 110°bertanda negatif.

Contoh 2:

Tentukan nilai perbandingan trigonometri apabila α adalah sudut yang dibentuk oleh titik
A(-6, -8) dan sumbu X.

Penyelesaian:

Permasalahan di atas dapat diilustrasikan sebagai berikut:

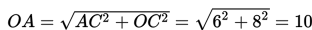
Oleh karena titik A(-6, -8) terletak di kuadran III, maka nilai perbandingan trigonometri dari sudut yang dibentuk oleh titik A(-6, -8) dan sumbu X adalah sebagai berikut:

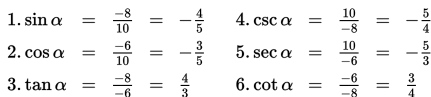
Contoh 3:

Diketahui cos α=−513 dan π<α<32π. Tentukan nilai tan α.

Penyelesaian:

Oleh karena π<α<32π, maka α terletak di kuadran III.

Dengan demikian,

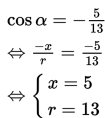
Selanjutnya, karena x2+y2=r2, maka

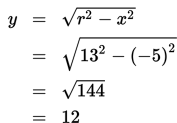
Dengan demikian, tan α=−y−x=−12−5=125.