PERTIDAKSAMAAN NILAI MUTLAK (SMA)

Sebelum mempelajari pertidaksamaan nilai mutlak, marik kita ingat kembali definisi mengenai nilai mutlak. Nilai mutlak dari x secara aljabar didefinisikan sebagai berikut :

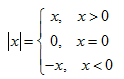
Selain itu, perlu kalian ingat bahwa untuk setiap bilangan x real, berlaku :

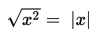
Berdasarkan konsep tersebut, maka dapat kita turunkan teorema mengenai pertidaksamaan nilai mutlak. Pertidaksamaan nilai mutlak adalah pertidaksamaan yang variabelnya berada di dalam tanda mutlak.

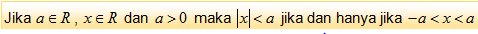
Bukti

Untuk membuktikan teorema ini, kita perlu membuktikannya menjadi dua arah yaitu :
jika |x| < a maka -a < x < a dan jika -a < x < a maka |x| < a

Untuk menyelesaikan pertidaksamaan nilai mutlak, kalian dapat menggunakan sifat-sifat berikut :

• Pertidaksamaan |ax +b | < c dimana c > 0 ekuivalen dengan -c < ax + b < c

• Pertidaksamaan |ax +b | > c dimana c > 0 ekuivalen dengan ax + b < -c atau ax + b > c

• Bentuk a < |f(x)| < b dimana a > 0 dan b > 0 ekuivalen dengan a < f(x) < b atau -b < f(x) < -a

• Bentuk |f(x)| > |g(x)| ekuivalen dengan |f(x)|2 > |g(x)|2 atau [f(x) + g(x)] [f(x) - g(x)] > 0

Untuk memperdalam pemahaman kalian, mari kita cermati beberapa contoh berikut ini :

Contoh 1 : Menyelesaikan pertidaksamaan dalam bentuk |ax + b|

Carilah nilai x yang memenuhi |2x + 5| < 17

Penyelesaian :

Untuk menyelesaiakan soal di atas, ikutilah langkah-langkah berikut ini :

1. tuliskan bentuk ketidaksamaannya -> |2x + 5| < 17
2. tuliskan bentuk ekuivalennya -> -17 < 2x + 5 < 17
3. kurangkan tiap suku dengan 5 -> -22 < 2x < 12
4. bagilah tiap suku dengan 2 -> -11 < x < 6

Penyelesaian pertidaksamaan di atas dapat digambarkan dengan garis bilangan berikut ini :

Contoh 2: Menyelesaikan pertidaksamaan dalam bentuk |f(x)| > |g(x)|

Carilah nilai x yang memenuhi |2x - 1| > |x + 3|

Penyelesaian :

1. tuliskan bentuk ketidaksamaannya -> |2x - 1| > |x + 3|
2. tuliskan bentuk ekuivalennya -> [ (2x - 1) + (x + 3) ] [ (2x - 1) - (x + 3) ] > 0
3. operasikan nilai yang ada dalam kurung -> [ 3x + 2 ] [ x - 4 ] > 0
4. selesaikan pertidaksamaan -> x < 2/3 atau x > 4