Teorema Pythagoras pada Sisi-Sisi Segitiga Siku-Siku
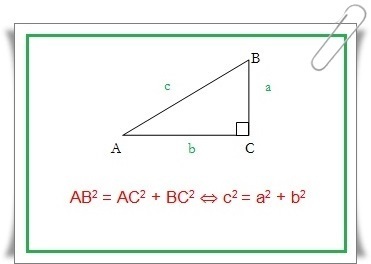
Misalnya, pada ∆ABC yang siku-siku di C, berlaku:
Contoh 1
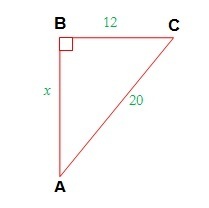
Coba tentukan nilai x pada bangun berikut.
Jawab:
Dapat kamu amati bahwa ∆ABC siku-siku di B sehingga:
AC2 = AB2 + BC2
⇔ 202 = x2 + 122
⇔400 = x2 + 144
⇔x2 = 400 – 144
⇔x2 = 256
⇔x = 256−−−√
⇔x = 16
Jadi, x = 16.
Tripel Pythagoras
Untuk menentukan salah satu sisi pada segitiga siku-siku dengan cepat dapat dilakukan dengan mudah dan tanpa menggunakan teorema Pythagoras. Caranya kamu dapat menggunakan tripel Pythagoras.

Berikut ini daftar tripel Pythagoras.

Pasangan tripel ini berlaku untuk kelipatannya.
Contoh 2
Buktikan bahwa 12, 5, 13 merupakan tripel Pythagoras.
Jawab:
Misalkan a = 12, b = 5, dan c = 13.
Berarti, a2 = 144, b2 = 25, dan c2 = 169.
Kamu dapat mengamati bahwa a2 + b2 = 144 + 25 = 169.
Jadi, c2 = a2 + b2 .
Ini berarti, 12, 5, 13 memenuhi teorema Pythagoras sehingga ketiga bilangan tersebut merupakan tripel Pythagoras.
Menentukan Jenis Segitiga jika Diketahui Panjang Sisi-Sisinya
Menurut teorema Pythagoras, pada ∆ABC yang siku-siku di C, berlaku c2 = a2 + b2 . Pernyataan tersebut berlaku juga sebaliknya, yaitu jika pada ∆ABC diketahui c2 = a2 + b2 maka ∆ABC merupakan segitiga siku-siku di C. Kebalikan teorema Pythagoras ini dapat digunakan untuk menyelidiki apakah sebuah segitiga merupakan segitiga siku-siku atau bukan.
Selengkapnya mengenai jenis-jenis segitiga jika diketahui panjang sisinya, yaitu sebagai berikut.

Contoh 3
Coba selidiki apakah ∆ABC dengan panjang sisi 15 cm, 36 cm, dan 39 cm merupakan segitiga siku-siku.
Jawab:
Sisi terpanjang pada ∆ABC memiliki panjang 39 cm. Kamu dapatkan 392 = 1.521.
Sisi-sisi lainnya memiliki panjang 15 cm dan 36 cm. Kamu dapatkan 152 = 225 dan 362 = 1.296.
Coba perhatikan bahwa 152 + 362 = 225 + 1.296 = 1.521.
Jadi, 152 + 362 = 392 .
Oleh karena pada ∆ABC sisi-sisinya memenuhi teorema Pythagoras, maka ∆ABC merupakan segitiga siku-siku.
0 komentar:
Post a Comment