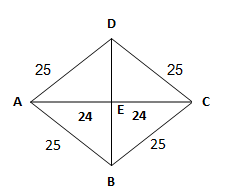
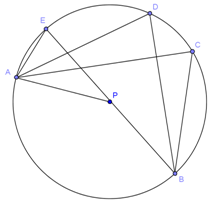
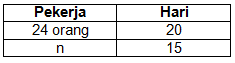
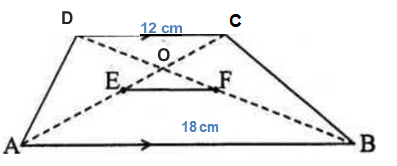
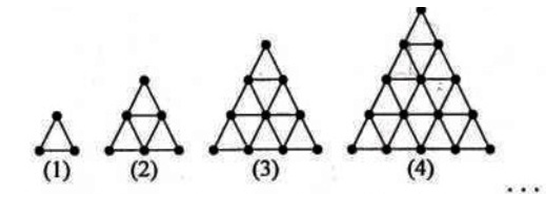
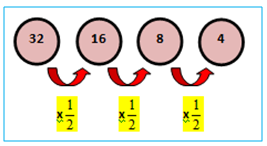
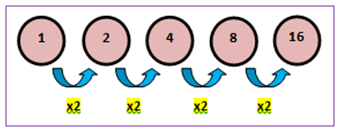
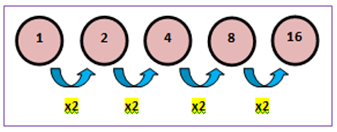
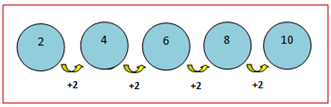
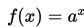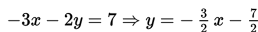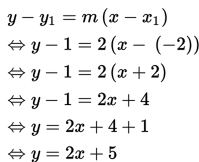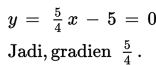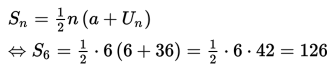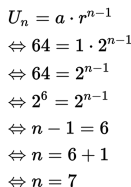Sunday, January 31, 2016

MENAFSIRKAN BENTUK ALJABAR SEDERHANA

Kalian mungkin tahu apa yang disebut dengan polinomial. Polinomial adalah sebuah ekspresi dengan satu atau lebih variabel dan koefisien-koefisiennya, seperti f(x) =3x2+4 misalnya. Ada dua konsep penting untuk memahami ekspresi-ekspresi ini. Koefisien dan suku. Sebuah koefisien secara mendasar adalah sebuah suku pilihan untuk bilangan didepan sebuah variabel. Dalam persamaan pendahuluan, f(x), koefisien dari x2 adalah 3. Suku-sukunya adalah sekedar bilangan dari “hal-hal,” dapat berupa bilangan atau variabel, di dalam ekspresi. Fungsi contoh kita, f(x)= 3x2+4, memiliki dua suku, 3x2 dan 4.

Polinomial dengan bilangan suku tertentu memiliki nama-nama khusus. Sebuah ekspresi dengan hanya satu suku disebut sebagai sebuah monomial, seperti g(x) =2x4. Jika ekspresinya memiliki dua suku, seperti p(x) =3x2-4, disebut dengan binomial, dan sebuah ekspresi dengan tiga suku disebut dengan trinomial. Penting untuk diingat bahwa bilangan suku-suku tersebut tidak didasarkan pada variabel. Mari kita gunakan fungsi q(x) =x2t+7s sebagai contoh kita. Kalian mungkin tergoda untuk menyebut ekspresi ini sebuah trinomial karena memiliki tiga variabel, x, t, dan s. Namun ekspresi ini adalah sebuah binomial. Kunci untuk memahami ekspresi ini adalah dengan mengenali bahwa x2t adalah sebuah suku tunggal meskipun memiliki dua variabel.

Sekarang mari bahas beberapa contoh untuk mengisi konsep apapun yang mungkin kita lewatkan

Pertanyaan 1: Berikut ini manakah yang BUKAN sebuah suku polinomial?

A) 2x2

B) 3x-2

C) 9x5

D) x

E) 17x4

Penjelasan: Reaksi awal kalian mungkin akan menganggap bahwa ini adalah sebuah pertanyaan jebakan, semua kelihatannya polinomial, bukan begitu? Namun kuncinya adalah mengingat bahwa ekspresi-ekspresi polinomial hanya dapat dinaikkan pada bilangan cacah positif. Oleh karena itu, polinomial apapun yang dinaikkan pada eksponen pecahan, desimal, atau negatif, bukanlah sebuah ekspresi polinomial. Mengetahui ini, pilihan yang benar adalah B, 3x-2.

Pertanyaan 2: Dari persamaan berikut ini manakah yang memiliki enam sebagai koefisien utama?

A) 2x2+6x+6

B) x4+6

C) 9x6-6

D) 6x-2

E) 17x6-x5+2x4-2x2+6x+6

Penjelasan: Sebuah koefisien utama adalah sekedar koefisien pada suku pertama dari ekspresi polinomial. Pertanyaan ini mengharuskan persamaan dengan koefisien utama enam, dan satu-satunya yang memenuhi pertanyaan ini adalah D, 6x-2.

Menyelesaikan sebuah sistem persamaan linier dan sebuah persamaan kuadrat secara aljabar

Menyelesaikan sebuah sistem persamaan linier dan sebuah persamaan kuadrat secara aljabar

Sebuah persamaan kuadrat didefinisikan sebagai sebuah persamaan dimana satu atau lebih sukunya dipangkatkan tapi tidak dinaikkan pada pangkat tinggi. Bentuknya adalah parabolik.

Bentuk umumnya adalah ax2 + bx + c = 0, dimana a, b dan c adalah konstanta.

Penyelesaian dari sebuah sistem kuadrat linier ada pada titik perpotongan dari dua garis yang digambarkan bersama-sama.

Ada tiga kemungkinan perpotongan dari kedua grafik tersebut:

1. Kedua grafik tersebut berpotongan pada dua titik.

Daalam kasus ini, ada dua penyelesaian real dari sistem ini. Sebuah contoh ditunjukkan dalam gambar dibawah.

2. Persamaan liniernya adalah garis singgung terhadap persamaan kuadrat.

Dalam kasus ini, hanya ada satu penyelesaian real dari sistem ini. Contohnya

ditunjukkan dalam gambar dibawah.

3. Kedua grafik tidak berpotongan sama sekali.

Dalam kasus ini, tidak ada penyelesaian real karena grafik-grafiknya tidak

berpotongan. Contohnya ditunjukkan dalam gambar dibawah ini.

Kuis ini adalah mengenai sistem penyelesaian dari persamaan-persamaan linier-kuadrat secara aljabar . Sejumlah contoh disediakan di bawah ini yang akan membantu kalian menjelaskan konsep-konsep kalian lebih lanjut.

CONTOH 1:

Selesaikan sistem persamaan ini secara aljabar:
x2 + y2 = 26 (persamaan kuadrat dari bentuk x2 + y2 = r2: lingkaran)
x - y = 6 (persamaan linear)

PENYELESAIAN:

LANGKAH 1:

Tentukan persamaan linier untuk salah satu variabel.

x - y = 6
x = y + 6

LANGKAH 2:

Substitusi nilai ini ke dalam persamaan kuadrat.

x2 + y2 = 26
(y + 6)2 + y2 = 26
y2 + 12y + 36 + y2 = 26
2y2 + 12y + 36 = 26
2y2 + 12y + 10 = 0

y2 + 6y + 5 = 0

(y + 5)(y +1) = 0
y + 5=0 y + 1=0
y = -5 y = -1

LANGKAH 3:

Substitusi kembali nilai-nilai ini ke dalam persamaan linier untuk mendapatkan nilai-nilai dari variabel yang lainnya.

x - y = 6

x - (-5) = 6
x + 5 = 6
yang memberikan x = 1

x - y = 6

x - (-1) = 6
x + 1 = 6
yang memberikan x = 5

Jadi,

Himpunan Penyelesaian = {(1,-5),(5,-1)}

CONTOH 2:

Pada berapa banyak titik persamaan-persamaan linier dan kuadrat berikut ini berpotongan?

y = x2 + 2x + 1

y = x - 1

PENYELESAIAN:

Menyamakan kedua persamaan, kita mendapatkan

x2 + 2x + 1 = x - 1

x2 + x + 2 = 0

Sekarang carilah diskriminannya:

= b2 - 4ac

= 12 - 4(1)(2)

= 1 - 8

= -7

Kita tahu bahwa,

Jika diskriminannya = 0 (satu titik perpotongan)
Jika diskriminannya > 0 (dua titik perpotongan)
Jika diskriminannya < 0 (tidak ada titik perpotongan)

Karena, Diskriminan < 0

Jadi, kita dapat mengatakan bahwa sistem tersebut tidak memiliki penyelesaian real.

Menyelesaikan sistem persamaan yang terdiri atas persamaan linear dan persamaan kuadrat dengan menggunakan grafik

Menyelesaikan sistem persamaan yang terdiri atas persamaan linear dan persamaan kuadrat dengan menggunakan grafik

Persamaan kuadrat didefinisikan sebagai suatu persamaan dengan sebuah suku atau beberapa suku berderajat derajat 2 dan tidak ada suku yang mempunyai derajat lebih dari 2. Dengan demikian, bentuknya adalah parabola.

Adapun bentuk umumnya adalah : ax2 + bx + c = 0, dimana a, b, dan c adalah suatu konstanta.

Penyelesaian dari suatu sistem persamaan kuadrat-linear merupakan titik potong antara grafik kuadrat dan grafik linear.

Dengan demikian, ada 3 kejadian yang mungkin, yaitu :

1. Dua grafik berpotongan pada 2 buah titik.

Dalam kasus ini, sistem persamaan mempunyai 2 penyelesaian real. Contoh : :

2. Grafik linear menyinggung grafik kuadrat.

Dalam kasus ini, sistem persamaan mempunyai tepat satu penyelesaian real. Berikut ini

adalah contohnya :

3. Dua grafik tidak berpotongan sama sekali.

Dalam kasus ini, tidak ada penyelesaian real yang diperoleh. Hal ini terjadi karena kedua grafik

tidak berpotongan. Berikut ini adalah contohnya :

Dalam pelajaran ini, kalian akan belajar tentang bagaimana cara menyelesaikan suatu sistem persamaan yang terdiri atas persamaan linear dan persamaan kuadrat dengan menggunakan grafik. Berikut ini adalah beberapa contoh yang akan membantu kalian memahami materi ini :

CONTOH

Dari 3 gambar berikut ini, manakah yang merupakan sistem persamaan dengan jumlah penyelesaian real paling sedikit?

PENYELESAIAN :

Pada gambar C tidak ditemukan titik potong antara kurva dan garis. Dengan demikian, sistem pada gambar C mempunyai jumlah penyelesaian real yang paling sedikit, yaitu nol.

MEMBANDINGKAN FUNGSI-FUNGSI EKSPONENSIAL

Pada pelajaran ini, kita akan membandingkan berbagai macam bentuk persamaan eksponensial untuk menentukan mana yang tumbuh atau berkurang lebih cepat. Kita akan membandingkan 3 bentuk, aljabar, grafik, dan kalimat.

Pertama-tama, ingat kembali bahwa bentuk dasar persamaan eksponensial adalah,

y=A(b)x di mana A adalah nilai awal dan b adalah tingkat pertumbuhan/penurunan. Juga ingat kembali bahwa fungsi eksponensial terlihat seperti berikut,

Sekarang untuk beberapa perbandingan.

Contoh 1: Dari pilihan berikut ini, manakah yang mempunyai tingkat pertumbuhan yang paling tinggi?

Di sini kita dapat melihat bahwa garis hijau mempunyai tingkat pertumbuhan yang paling besar karena ini yang paling curam. Meskipun garis biru dimulai lebih tinggi kita melihat bahwa garis biru akan diambil alih oleh garis hijau, yang mengindikasikan bahwa garis hijau lebih curam.

Contoh 2: Dari pilihan berikut manakah yang mempunyai tingkat penurunan yang lebih cepat?

y=5(3)-x di mana x dalam jam, atau

sebuah material radioaktif kehilangan setengah dari massanya setiap jam.

Dalam kasus ini persamaan aljabar mempunyai tingkat penurunan yang lebih cepat karena ia kehilangan (2/3)nya setiap jam. Secara alternatif kita dapat mengubah permasalahan dalam suatu kalimat ke suatu persamaan aljabar dan akan menjadi y=A(2)-x. Jadi karena 3>2 kita tahu bahwa persamaan dengan 3 menurun lebih cepat.

Contoh 3: Dari pilihan berikut ini manakah yang mempunyai tingkat pertumbuhan yang lebih cepat?

y=5x ataukah grafik persamaan di bawah ini?

Kita melihat bahwa grafik di atas melalui titik (0,1) dan (1,2). Karena grafik fungsi di atas adalah grafik eksponensial persamaan maka persamaan grafik di atas tentunya y=2x. Karena 5>2 maka dapat kita simpulkan bahwa persamaan aljabar harus mempunyai tingkat pertumbuhan yang lebih cepat.

MENGGAMBARKAN HUBUNGAN DENGAN GRAFIK

Pada bagian ini kita akan belajar bagaimana cara menggambar grafik dari berbagai jenis hubungan meliputi hubungan linear, kuadrat dan perpangkatan. Kemudian kita akan belajar bagaimana cara membuat hubungan linear dari sebuah soal cerita.

Sebuah hubungan linear memiliki bentuk y = mx + b dimana m adalah kemiringan dan b adalah perpotongan sumbu y. Secara grafis, kemiringan mewakili seberapa curam garis tersebut, sedangkan b mewakili posisi awal (yaitu koordinat y jika x bernilai 0). Perhatikan dua grafik hubungan linier berikut:

Hubungan kuadrat mempunyai bentuk y=ax2+bx+c. . 'a' menentukan apakah parabola mengarah ke atas atau ke bawah dan 'c' menentukan perpotongan sumbu y lagi. Perhatikan dua grafik persamaan kuadrat berikut ini:

Terakhir, kita akan melihat hubungan perpangkatan. Hubungan perpangkatan memperagakan pertumbuhan atau peluruhan seperti pertumbuhan dari kota atau peluruhan karbon dari waktu ke waktu. Fungsi perpangkatan mempunyai bentuk y=P(b)x . P merupakan nilai awal benda (bisa berupa populasi atau materi atau apa pun yang sedang diperagakan) sedangkan b mewakili tingkat pertumbuhan atau peluruhan (yaitu seberapa cepat benda tersebut tumbuh atau meluruh). Perhatikan dua grafik perpangkatan berikut (pertama adalah pertumbuhan dan kemudian peluruhan)

Selanjutnya, kita akan melihat bagaimana cara membangun sebuah model linier dari sebuah soal cerita.
Contoh 1: Seorang siswa mampu membaca 50 halaman per jam. Saat ini dia sedang membaca halaman 20. Berapa lama waktu yang dibutuhkan siswa tersebut untuk membaca buku setebal 370 halaman?

Pertama, kita perlu membuat persamaan dari soal tersebut. Siswa tersebut membaca 50 halaman per jam, dan ini dianggap kemiringan. Saat ini dia berada di halaman 20, yang merupakan perpotongan sumbu y. Maka, persamaan dari soal tersebut adalah y = 50x +20, dimana y adalah jumlah halaman yang dibaca dan x adalah jumlah jam yang diperlukan untuk membaca. Persamaannya akan ditampilkan di bawah ini,

Untuk mengetahui berapa lama waktu yang dibutuhkan untuk membaca buku itu, anggap nilai y = 370 masukkan ke dalam rumus untuk mencari x. Maka akan menjadi,,

370=50x+20

350=50x

x=7

Maka siswa tersebut membutuhkan waktu 7 jam untuk membaca seluruh buku tersebut.

GRAFIK FUNGSI EKSPONESIAL DAN LOGARITMA

Dalam pelajaran ini kita akan belajar menggambar grafik fungsi perpangkatan dan logaritma.

Pertama kita akan melihat metode menggambar grafik fungsi perpangkatan. Perhatikan penulisan fungsi perpangkatan berikut:

Mari kita menggambar grafik dari fungsi berikut:

Kita akan membuat tabel untuk nilai 'x' dan 'f (x)' yang berbeda

Sekarang buatlah titik-titik dan hubungkan mereka dengan kurva halus seperti yang ditunjukkan pada gambar untuk mendapatkan grafik yang diperlukan.

Dari grafik ini, kita dapat mengamati beberapa ciri-ciri grafik fungsi perpangkatan sepertif(x)=ax

Jika a>1

(i) ax selalu positif untuk semua nilai nyata x.

(ii) ax=1 , jika x=0.

(iii) ax akan meningkat ketika x juga meningkat

(iv) ax→ 0 seiring dengan x→ -∞ .

Sekarang mari kita membuat grafik f(x)=ex

Kita tahu bahwa nilai e kira-kira adalah 2.718

Grafik ini akan memiliki sifat yang sama seperti f(x)=ax jika a>1.

Kita akan menyiapkan tabel nilai x dan f(x) seperti contoh dibawah ini:

Sekarang buatlah titik-titik pada bidang koordinat dan hubungkan dengan mereka untuk mendapatkan kurva yang halus.

Sekarang kita akan membahas grafik logaritmik. Jika,

x = 10y

Ambillah log pada kedua sisi persamaan.

log x = log 10y

log x = y log 10

log x = y (1)

Oleh karena itu,,

y = log x

Berhubung x = 10y , maka kita dapat melihat bahwa

Untuk semua nilai nyata y

10y > 0

Ini berarti bahwa x>0

Makalog x hanya ada ketika x>0

Jadi kita hanya akan mengambil nilai-nilai positif dari x, itu berarti bahwa domain log x hanyalah bilangan nyata positif..

Untuk menggambar grafik y = log x, kita akan membuat tabel nilai dari x dan y.

Gambarlah titik-titik dan hubungkan mereka untuk mendapatkan kurva dari y = log x.

Demikian pula grafik logaritma natural dapat ditarik dengan mencari nilai-nilai x dan f(x) dan menghubungkan mereka.

Saturday, January 30, 2016

SOAL DAN PEMBAHASAN UJIAN NASIONAL SMP TAHUN 2011/2012 NO 31 - 40

Soal 31

Diketahui keliling belahketupat 100 cm dan panjang salah satu diagonalnya 48 cm. Luas belahketupat tersebut adalah ….

Sunday, January 31, 2016

Saturday, January 30, 2016

Friday, January 29, 2016

Soal 21

Soal 11

Thursday, January 28, 2016

Soal 1

Wednesday, January 27, 2016

Soal 31

Soal 21

Tuesday, January 26, 2016

Monday, January 25, 2016

Soal 11

Soal 1

Sunday, January 24, 2016

Soal 31

Soal 21

Soal 1

Saturday, January 23, 2016

Thursday, January 21, 2016

Wednesday, January 20, 2016

Tuesday, January 19, 2016

Saturday, January 16, 2016

Thursday, January 14, 2016

Tuesday, January 12, 2016

Sunday, January 10, 2016

Saturday, January 9, 2016

Deret Turun

Deret Naik

DERET GEOMETRI

Friday, January 8, 2016

Contoh 1

DERET ARITMETIKA

Wednesday, January 6, 2016

GARIS SINGGUNG PERSEKUTUAN DALAM

GARIS SINGGUNG PERSEKUTUAN LUAR