DERET GEOMETRI 

      Sebelum membahas mengenai deret geometri, ada baiknya kita mengingat kembali tentang barisan geometri. Apakah kamu masih ingat tentang barisan geometri? Pada topik sebelumnya telah dibahas bahwa suatu barisan disebut barisan geometri, jika untuk setiap bilangan asli n berlaku,

      UnUn−1=r
Dengan,
Un=arn–1 = suku ke-n
Un−1 = suku ke-(n - 1)
r = rasio atau perbandingan
a = suku pertama

Contoh barisan geometri adalah, 1, 2, 4, 8, 16, ….Untuk lebih jelasnya, perhatikan ilustrasi berikut.

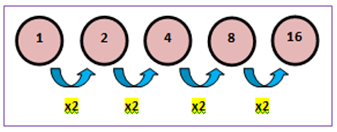
Dari ilustrasi di atas diperoleh informasi bahwa suku pertama barisan tersebut adalah a = 1 dan rasio antar sukunya adalah r = 2.

      Apa hubungan antara barisan geometri dan deret geometri? Jika U1,U2,U3,...Un adalah suku-suku barisan geometri, maka U1+U2+U3+...+Un disebut deret geometri.Jadi, suku-suku dari suatu deret geometri berasal dari barisan geometri. Misalnya, pada contoh di atas telah diketahui bahwa 1, 2, 4, 8, 16, … merupakan barisan geometri, maka 1 + 2 + 4 + 8 + 16 + … merupakan deret geometri. Dengan demikian diperoleh bentuk umum untuk deret geometri, yaitu:
      a+ar+ar2+ar3+...

Dengan,
a = suku pertama
r= rasio atau perbandingan

      Seperti deret aritmetika, untuk menentukan jumlah n suku suatu deret geometri akan sangat tidak efektif apabila kita menjumlahkan suku-sukunya satu persatu. Hal ini karena membutuhkan waktu yang lebih lama dan sering terjadi kesalahan. Untuk itu, dibutuhkan cara khusus untuk menghitung jumlah n suku pertama (Sn) suatu deret geometri. Ada dua rumus yang digunakan untuk menghitung Sn suatu deret geometri. Penggunaan rumus tersebut tergantung jenis deret geometrinya. Berikut diuraikan jenis-jenis deret geometri beserta rumus Sn yang digunakan.