GRAFIK FUNGSI EKSPONESIAL DAN LOGARITMA

Dalam pelajaran ini kita akan belajar menggambar grafik fungsi perpangkatan dan logaritma.

Pertama kita akan melihat metode menggambar grafik fungsi perpangkatan. Perhatikan penulisan fungsi perpangkatan berikut:

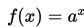
Mari kita menggambar grafik dari fungsi berikut:

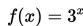
Kita akan membuat tabel untuk nilai 'x' dan 'f (x)' yang berbeda

Sekarang buatlah titik-titik dan hubungkan mereka dengan kurva halus seperti yang ditunjukkan pada gambar untuk mendapatkan grafik yang diperlukan.

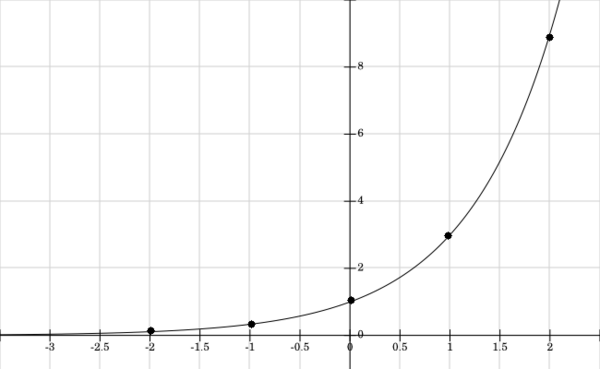
Dari grafik ini, kita dapat mengamati beberapa ciri-ciri grafik fungsi perpangkatan sepertif(x)=ax

Jika a>1

(i)                  ax   selalu positif untuk semua nilai nyata x.

(ii)                ax=1 , jika x=0.

(iii)               ax  akan meningkat ketika x juga meningkat

(iv)              ax→ 0  seiring dengan x→ -∞ .

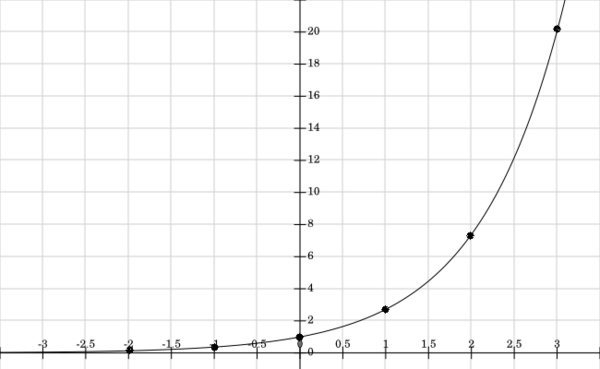
Sekarang mari kita membuat grafik f(x)=ex 

Kita tahu bahwa nilai e kira-kira adalah 2.718

Grafik ini akan memiliki sifat yang sama seperti f(x)=ax jika a>1.

Kita akan menyiapkan tabel nilai x dan f(x) seperti contoh dibawah ini:

Sekarang buatlah titik-titik pada bidang koordinat dan hubungkan dengan mereka untuk mendapatkan kurva yang halus.

Sekarang kita akan membahas grafik logaritmik. Jika,

x = 10y

Ambillah log pada kedua sisi persamaan.

log x = log 10y

log x = y log 10 

log x = y (1)

Oleh karena itu,,

y = log x

Berhubung x = 10y , maka kita dapat melihat bahwa 

Untuk semua nilai nyata y

10y > 0 

Ini berarti bahwa x>0

Makalog x hanya ada ketika x>0

Jadi kita hanya akan mengambil nilai-nilai positif dari x, itu berarti bahwa domain log x hanyalah bilangan nyata positif..

Untuk menggambar grafik y = log x, kita akan membuat tabel nilai dari x dan y.

Gambarlah titik-titik dan hubungkan mereka untuk mendapatkan kurva dari y = log x.

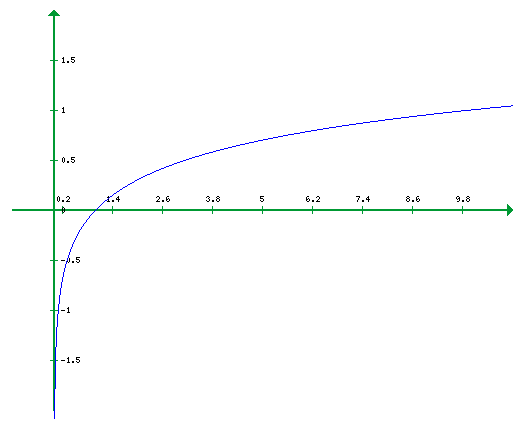
Demikian pula grafik logaritma natural dapat ditarik dengan mencari nilai-nilai x dan f(x) dan menghubungkan mereka.