Pada pelajaran ini, kita akan membandingkan berbagai macam bentuk persamaan eksponensial untuk menentukan mana yang tumbuh atau berkurang lebih cepat. Kita akan membandingkan 3 bentuk, aljabar, grafik, dan kalimat.
Pertama-tama, ingat kembali bahwa bentuk dasar persamaan eksponensial adalah,
y=A(b)x di mana A adalah nilai awal dan b adalah tingkat pertumbuhan/penurunan. Juga ingat kembali bahwa fungsi eksponensial terlihat seperti berikut,
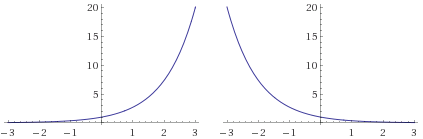
Sekarang untuk beberapa perbandingan.
Contoh 1: Dari pilihan berikut ini, manakah yang mempunyai tingkat pertumbuhan yang paling tinggi?
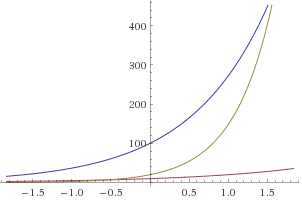
Di sini kita dapat melihat bahwa garis hijau mempunyai tingkat pertumbuhan yang paling besar karena ini yang paling curam. Meskipun garis biru dimulai lebih tinggi kita melihat bahwa garis biru akan diambil alih oleh garis hijau, yang mengindikasikan bahwa garis hijau lebih curam.
Contoh 2: Dari pilihan berikut manakah yang mempunyai tingkat penurunan yang lebih cepat?
y=5(3)-x di mana x dalam jam, atau
sebuah material radioaktif kehilangan setengah dari massanya setiap jam.
Dalam kasus ini persamaan aljabar mempunyai tingkat penurunan yang lebih cepat karena ia kehilangan (2/3)nya setiap jam. Secara alternatif kita dapat mengubah permasalahan dalam suatu kalimat ke suatu persamaan aljabar dan akan menjadi y=A(2)-x. Jadi karena 3>2 kita tahu bahwa persamaan dengan 3 menurun lebih cepat.
Contoh 3: Dari pilihan berikut ini manakah yang mempunyai tingkat pertumbuhan yang lebih cepat?
y=5x ataukah grafik persamaan di bawah ini?
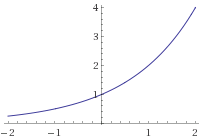
Kita melihat bahwa grafik di atas melalui titik (0,1) dan (1,2). Karena grafik fungsi di atas adalah grafik eksponensial persamaan maka persamaan grafik di atas tentunya y=2x. Karena 5>2 maka dapat kita simpulkan bahwa persamaan aljabar harus mempunyai tingkat pertumbuhan yang lebih cepat.
0 komentar:
Post a Comment