Menyelesaikan sebuah sistem persamaan linier dan sebuah persamaan kuadrat secara aljabar
Sebuah persamaan kuadrat didefinisikan sebagai sebuah persamaan dimana satu atau lebih sukunya dipangkatkan tapi tidak dinaikkan pada pangkat tinggi. Bentuknya adalah parabolik.
Bentuk umumnya adalah ax2 + bx + c = 0, dimana a, b dan c adalah konstanta.
Penyelesaian dari sebuah sistem kuadrat linier ada pada titik perpotongan dari dua garis yang digambarkan bersama-sama.
Ada tiga kemungkinan perpotongan dari kedua grafik tersebut:
1. Kedua grafik tersebut berpotongan pada dua titik.
Daalam kasus ini, ada dua penyelesaian real dari sistem ini. Sebuah contoh ditunjukkan dalam gambar dibawah.
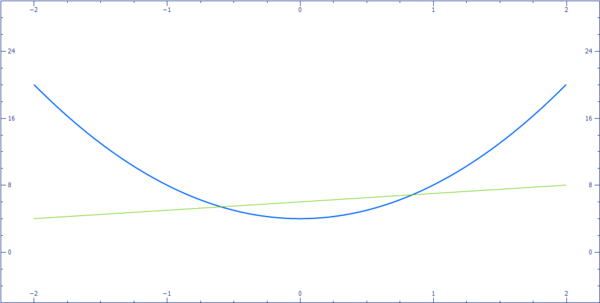
2. Persamaan liniernya adalah garis singgung terhadap persamaan kuadrat.
Dalam kasus ini, hanya ada satu penyelesaian real dari sistem ini. Contohnya
ditunjukkan dalam gambar dibawah.
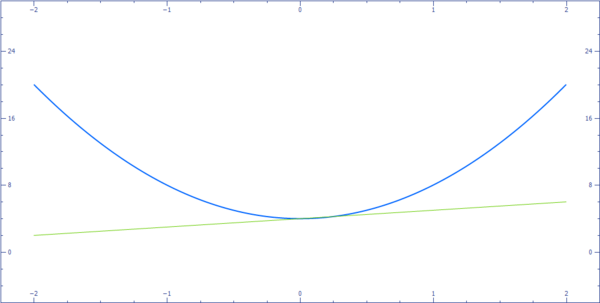
3. Kedua grafik tidak berpotongan sama sekali.
Dalam kasus ini, tidak ada penyelesaian real karena grafik-grafiknya tidak
berpotongan. Contohnya ditunjukkan dalam gambar dibawah ini.
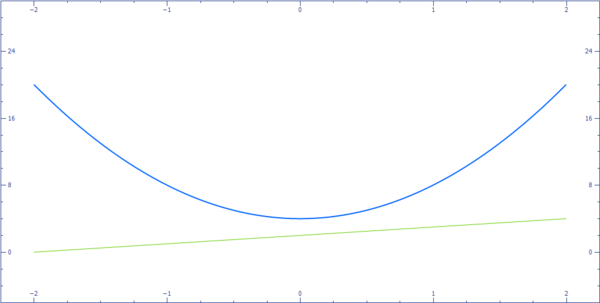
Kuis ini adalah mengenai sistem penyelesaian dari persamaan-persamaan linier-kuadrat secara aljabar . Sejumlah contoh disediakan di bawah ini yang akan membantu kalian menjelaskan konsep-konsep kalian lebih lanjut.
CONTOH 1:
Selesaikan sistem persamaan ini secara aljabar:
x2 + y2 = 26 (persamaan kuadrat dari bentuk x2 + y2 = r2: lingkaran)
x - y = 6 (persamaan linear)
x2 + y2 = 26 (persamaan kuadrat dari bentuk x2 + y2 = r2: lingkaran)
x - y = 6 (persamaan linear)
PENYELESAIAN:
LANGKAH 1:
Tentukan persamaan linier untuk salah satu variabel.
x - y = 6
x = y + 6
x = y + 6
LANGKAH 2:
Substitusi nilai ini ke dalam persamaan kuadrat.
x2 + y2 = 26
(y + 6)2 + y2 = 26
y2 + 12y + 36 + y2 = 26
2y2 + 12y + 36 = 26
2y2 + 12y + 10 = 0
(y + 6)2 + y2 = 26
y2 + 12y + 36 + y2 = 26
2y2 + 12y + 36 = 26
2y2 + 12y + 10 = 0
y2 + 6y + 5 = 0
(y + 5)(y +1) = 0
y + 5=0 y + 1=0
y = -5 y = -1
y + 5=0 y + 1=0
y = -5 y = -1
LANGKAH 3:
Substitusi kembali nilai-nilai ini ke dalam persamaan linier untuk mendapatkan nilai-nilai dari variabel yang lainnya.
x - y = 6
x - (-5) = 6
x + 5 = 6
yang memberikan x = 1
x + 5 = 6
yang memberikan x = 1
x - y = 6
x - (-1) = 6
x + 1 = 6
yang memberikan x = 5
x + 1 = 6
yang memberikan x = 5
Jadi,
Himpunan Penyelesaian = {(1,-5),(5,-1)}
CONTOH 2:
Pada berapa banyak titik persamaan-persamaan linier dan kuadrat berikut ini berpotongan?
y = x2 + 2x + 1
y = x - 1
PENYELESAIAN:
Menyamakan kedua persamaan, kita mendapatkan
x2 + 2x + 1 = x - 1
x2 + x + 2 = 0
Sekarang carilah diskriminannya:
= b2 - 4ac
= 12 - 4(1)(2)
= 1 - 8
= -7
Kita tahu bahwa,
- Jika diskriminannya = 0 (satu titik perpotongan)
- Jika diskriminannya > 0 (dua titik perpotongan)
- Jika diskriminannya < 0 (tidak ada titik perpotongan)
Karena, Diskriminan < 0
Jadi, kita dapat mengatakan bahwa sistem tersebut tidak memiliki penyelesaian real.
0 komentar:
Post a Comment