SOAL DAN PEMBAHASAN UJIAN NASIONAL SMP TAHUN 2009/2010 NO 21 - 30

Soal 21

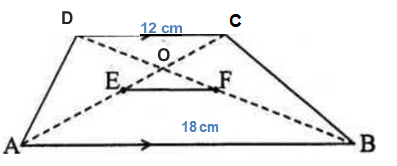
Perhatikan gambar bangun berikut.

Titik E dan F masing-masing titik tengah AC dan BD. Panjang EF adalah ....

 Pembahasan

Bangun tersebut adalah trapesium. Pada trapesium, kedua diagonalnya saling berpotongan sehingga menjadi dua potong dengan perbandingan masing-masing potongan sama dengan perbandingan sisi-sisi sejajarnya, yaitu:

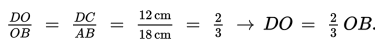
Misalkan DF = x , berarti FB = DF = x.

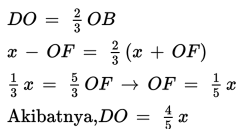
Perhatikan bahwa ∆DCO sebangun dengan ∆EFO sehingga:

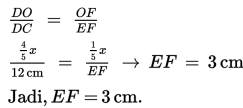
Soal 22

Sebuah karikatur berukuran 32 cm x 40 cm dipasang pada sebuah bingkai. Lebar bingkai bagian kiri dan kanan 4 cm. Jika karikatur dan bingkai sebangun, sedangkan Iebar bingkai bagian atas dan bawah sama, maka Iebar bingkai bagian bawah adalah ....

 Pembahasan

Perhatikan gambar berikut.

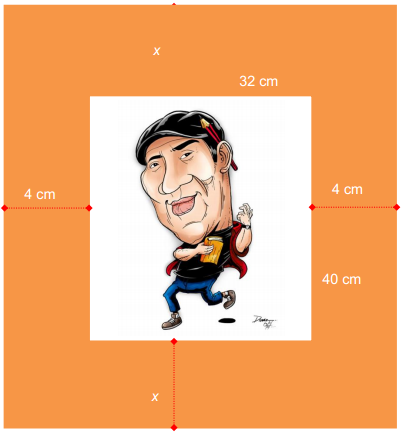
Dimisalkan x adalah lebar bingkai atas dan bawah.

Oleh karena karikatur dan bingkainya sebangun, maka:

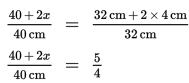
40 + 2x = 50 cm → x = 5 cm

Jadi, Iebar bingkai bagian bawah adalah 5 cm.

Soal 23

Perhatikan gambar berikut.

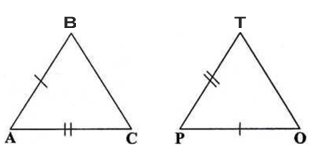
Segitiga ABC kongruen dengan segitiga POT. Pasangan sudut yang sama besar adalah ....

 Pembahasan

Segitiga ABC kongruen dengan segitiga POT, berarti:

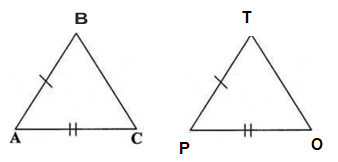
Jadi, besar ∠ABC dan ∠POT.

 Soal 24

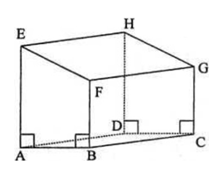
Perhatikan gambar di bawah ini.

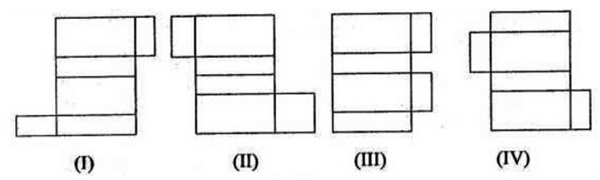
Rangkaian bangun yang merupakan jaring-jaring balok adalah ….

 Pembahasan

Rangkaian persegipanjang yang dapat dibentuk menjadi balok adalah sebagai berikut.

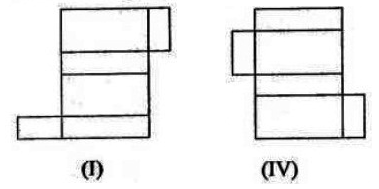
Soal 25

Perhatikan gambar belahketupat ABCD berikut ini.

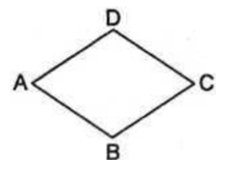
Jika besar ∠A : ∠B = 1 : 2, maka besar ∠C = ....

 Pembahasan

Pada belahketupat ABCD, ∠A + ∠B = 180⁰.

Oleh karena ∠A : ∠B = 1 : 2, maka ∠B = 2∠A.

Akibatnya, ∠A + ∠B = 180⁰ → ∠A + 2 ∠A = 180⁰.

Besar ∠A = 60⁰

Pada belahketupat ABCD, ∠C =∠A = 60⁰.

Jadi, besar ∠C = 60⁰.

 Soal 26

Perhatikan gambar berikut.

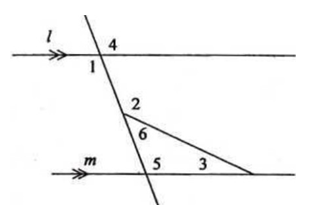
Besar sudut nomor 1 adalah 95⁰ dan besar sudut nomor 2 adalah 110⁰.
Besar sudut nomor 3 adalah ….

 Pembahasan

Perhatikan gambar berikut.

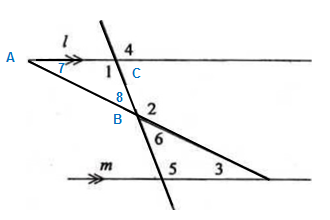
∠7 dan ∠3 adalah sepasang sudut berseberangan sehingga besar ∠7 = ∠3.

∠8 dan ∠6 saling bertolak belakang sehingga besar ∠8 = ∠6.

∠8 dan ∠2 saling berpelurus sehingga besar ∠8 + ∠2 = 180⁰.

Oleh karena ∠2 = 110⁰, maka ∠8 + 110⁰ = 180⁰ →∠8 = 70⁰.

Perhatikan ∆ABC. Pada ∆ABC berlaku:

∠7 + ∠8 + ∠1 = 180⁰
∠7 + 70⁰ + ∠95⁰ = 180⁰
∠7 = 15⁰

Oleh karena ∠7 = ∠3, maka ∠3 = 15⁰.

 Soal 27

Perhatikan gambar berikut ini.

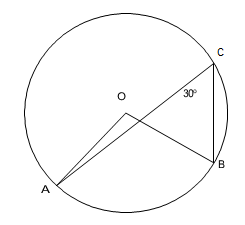
Diketahui O adalah titik pusat lingkaran. Besar sudutAOB adalah ....

 Pembahasan

∠AOB merupakan sudut pusat yang menghadap busur AB.

∠ACB merupakan sudut keliling yang juga menghadap busur AB.

Oleh karena sudut pusat dan sudut keliling menghadap busur yang sama, maka

∠AOB = 2 x ∠ACB = 2 x 30° = 60°.

Soal 28

Volume balok dengan panjang 3 cm, Iebar 5 cm, dan tinggi 12 cm adalah ....

 Pembahasan

Volume balok adalah V = p x l x t
                                          = 3 cm x 5 cm x 12 cm
                                          = 180 cm3

Jadi, volume balok adalah 180 cm3 .

Soal 29

Tabung dengan panjang jari-jari alas 10 cm berisi minyak setinggi 14 cm. Ke dalam tabung itu dimasukkan minyak lagi sebanyak 1,884 liter. Tinggi minyak dalam tabung sekarang adalah ....

 Pembahasan

Volume minyak yang ditambahkan adalah V = 1,884 liter = 1,884 dm3.

V = πr2 tt 
1,884 = 3,14 x 12 x tt 
tt = 0,6 dm = 6 cm

Jadi, tinggi minyak yang ditambahkan adalah 6 cm, sehingga tinggi minyak dalam tabung sekarang adalah 14 cm + 6 cm = 20 cm.

Soal 30

ABCD.EFGH pada gambar berikut ini adalah prisma dengan ABFE sejajar DCGH.

Panjang AB = 4 cm, BC = 6 cm, AE = 8 cm, dan BF = 5 cm. Luas permukaan prisma adalah ....

 Pembahasan

Terlebih dahulu, tentukan panjang EF.

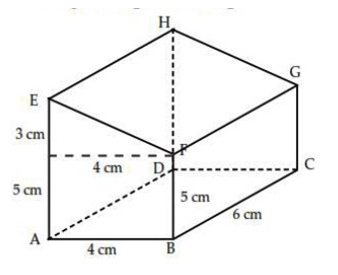
EF2 = 32 + 42 → EF = 5

Luas permukaan prisma = 2 Luas ABFE + Keliling ABFE x BC

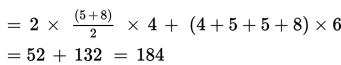
Jadi, luas permukaan prisma adalah 184 cm2 .