SOAL DAN PEMBAHASAN UJIAN NASIONAL SMP TAHUN 2011/2012 NO 11 - 20

Soal 11

Gradien garis -3x - 2y = 7 adalah ….

 Pembahasan

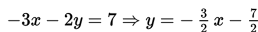
Jadi, gradien garisnya adalah

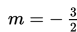
Soal 12

Persamaan garis melalui titik (- 2, 5) dan sejajar garis
x - 3y + 2 = 0 adalah ….

 Pembahasan

Kita tentukan terlebih dahulu gradien garisnya, yaitu

Persamaan garis melalui titik (x1, y1) dan sejajar garis yang bergradien m adalah y - y1 = m (x - x1), sehingga diperoleh

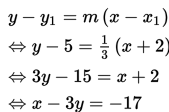
Jadi, persamaan garis melalui titik (- 2, 5) dan sejajar garis
x - 3y + 2 = 0 adalah x - 3y = -17

Soal 13

Faktor dari 49p2 - 64q2 adalah ....

 Pembahasan

Soal 14

Keliling suatu persegipanjang 28 cm. Jika panjangnya2 cm lebih dari lebarnya, luas persegipanjang tersebut adalah ….

 Pembahasan

Diketahui:

Keliling persegipanjang = K = 2p + 2l = 28 cm

Panjangnya 2 cm lebih dari lebarnya berarti p = 2 + l

Dengan demikian, kita peroleh

K   = 2p + 2l 
28 = 2 (2 + l ) + 2l
28 = 4 + 2l + 2l
24 = 4l
l    = 6 cm

Kita subsitusikan nilai l pada p = 2 + l, diperoleh nilai p = 2 + 6 = 8 cm

Luas = p x l = 8 x 6 = 48

Jadi, luas persegipanjang tersebut adalah 48 cm2 .

Soal 15

Diketahui rumus fungsi f (x) = -2x + 5. Nilai f (-4)adalah ….

 Pembahasan

f (x)   = -2x + 5
f (-4) = -2(-4) + 5 = 8 + 5 = 13

Soal 16

Diketahui f (x) = px + q, f (-1) = -5, dan f (4) = 5. Nilai f(-6) adalah ….

 Pembahasan

Diketahui:

f (x) = px + q

Dengan demikian,

f (-1) = -5 → -p + q = -5 ... (1)
f (4)  = 5  → 4p + q = 5  ... (2)

Kita lakukan eliminasi variabel q pada persamaan (1) dan (2), diperoleh:

-p + q  = -5
4p + q = 5 _
     -5p = -10
         p = 2

Selanjutnya subsitusikan nilai p pada persamaan (1)

-p + q   = -5
-(2) + q = -5
          q = -3

Nilai p = 2 dan nilai q = -3, akibatnya

f (x)   = px + q   = 2x - 3
f (-6) = 2(-6) - 3 = -12 - 3 = -15

Jadi, nilai f (-6) = -15.

Soal 17

Himpunan penyelesaian dari -7p + 8 < 3p - 22, untuk pbilangan bulat adalah …..

 Pembahasan

-7p + 8   < 3p - 22

-7p - 3p < -22 - 8

      -10p < -30       (kalikan dengan -1)

       10p > 30

            p > 3

Jadi, p = {4, 5, 6, ... }.

Soal 18

Jumlah tiga bilangan ganjil berurutan adalah 75. Jumlah bilangan terkecil dan terbesar bilangan tersebut adalah ….

 Pembahasan

Perhatikan 3 bilangan ganjil berurutan berikut : 1, 3, 5.

Jika kita perhatikan, selisih antara kedua bilangan ganjil yang berurutan adalah 2.

Dengan demikian, jika bilangan pertama kita misalkan dengan a, maka bilangan ke-2 dan ke-3 adalah a + 2 dan a + 4.

Diketahui:

Jumlah tiga bilangan ganjil berurutan adalah 75, berarti

a + a + 2 + a + 4 = 75

                 3a + 6 = 75

                       3a = 69

                         a = 23

Subsitusikan nilai a = 23 pada bilangan kedua dan ketiga, diperoleh

bilangan pertama = 23

bilangan kedua     = 23 + 2 = 25

bilangan ketiga     = 23 + 4 = 27

Dengan demikian, jumlah bilangan terkecil dan terbesar adalah 23 + 27 = 50.

Soal 19

Perhatikan gambar.

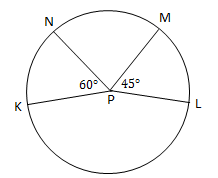
P adalah titik pusat lingkaran dan luas juring
PLM = 24 cm2. Luas juring PKN adalah ….

 Pembahasan

Kalian tentu masih ingat konsep perbandingan antara luas juring dan sudut pusat lingkaran, yaitu

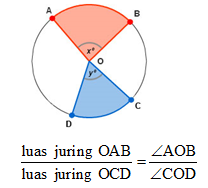
Dengan demikian,

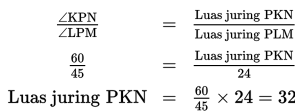
Jadi, Luas juring PKN adalah 32 cm2 .

 Soal 20

Dua buah lingkaran berpusat di A dan B dengan jarak 
AB = 20 cm. Panjang garis singgung persekutuan dalam 16 cm dan panjang jari-jari lingkaran dengan pusat A = 5 cm. Panjang jari-jari lingkaran dengan pusat B adalah ….

 Pembahasan

Perhatikan gambar berikut.

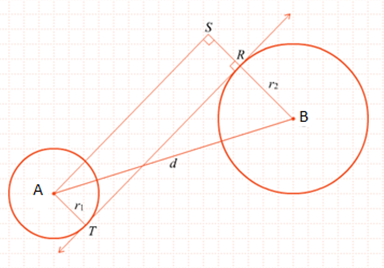
Diketahui:

d   = 20 cm
RT = 16 cm
r1  = 5 cm

Untuk menentukan r2, kita gunakan rumus garis singgung persekutuan dalam, yaitu

RT2         = d 2 - (r1 + r2)2
162         = 202 - (5 + r2)2
256        = 400 - (5 + r2)2
(5 + r2)2 = 144
5 + r2     = 12
r2           = 7

Jadi, panjang jari-jari lingkaran dengan pusat B adalah 7 cm.