Sudut Diantara Dua Tali Busur
- Sudut Diantara Dua Tali Busur yang Berpotongan di Dalam Lingkaran.
Perhatikan gambar lingkaran berikut.

Pada lingkaran O, ∠AOB, ∠BOC, ∠COD dan ∠DOA merupakan sudut pusat lingkaran. garis AC dan garis BD merupakan tali busur dari lingkaran yang berpotongan di dalam lingkaran pada titik E. Sehingga akan membentuk ∠AEB, ∠BEC, ∠CED dan ∠AED yang merupakan sudut - sudut dari perpotongan dua tali busur tersebut.
Oleh karena itu, berlaku persamaan
Oleh karena itu, berlaku persamaan
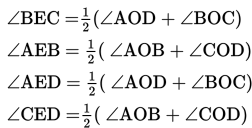
Berdasarkan persamaan di atas maka kita bisa menuliskan ∠AEB = ∠CED dan ∠BEC = ∠AED. Dengan demikian, dapat disimpulkan bahwa besar sudut diantara dua tali busur yang berpotongan di dalam lingkaran sama dengan setengah dari jumlah sudut-sudut pusat yang menghadap busur yang diapit oleh kaki-kaki sudut itu.
- Sudut Diantara Dua Tali Busur yang Berpotongan di Luar Lingkaran.
Perhatikan gambar lingkaran di bawah ini.

Pada lingkaran O di atas, ∠KOL, ∠LOM, ∠MON dan ∠NOK merupakan sudut pusat lingkaran. Sedangkan garis MN dan garis KL merupakan tali busur dari lingkaran yang berpotongan di luar lingkaran pada titik P. Sehingga akan membentuk ∠KPN yang merupakan sudut dari perpotongan dua tali busur tersebut.
Pada lingkaran di atas, ∠KMN merupakan sudut keliling yang menghadap busur KN, sehingga: ∠KMN= ½ ∠KON.
Sudut ∠MKL adalah sudut keliling yang menghadap busur LM, sehingga: ∠MKL = ½ ∠MOL
Perhatikan ∆KPM
Sudut ∠MKL adalah sudut luar ∆KPM, sehingga berlaku
Sudut ∠MKL adalah sudut luar ∆KPM, sehingga berlaku

Dari uraian di atas dapat disimpulkan bahwa besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah dari selisih sudut-sudut pusat yang menghadap busur yang diapit oleh kaki-kaki sudut itu.
Keren kak
ReplyDelete