Aturan Rantai

Misalkan y = f (u) dan u = g (x), y memiliki turunan di u dan u memiliki turunan di x sehingga, fungsi komposisi y = (f o g) (x) = f (g (x)) memiliki turunan di x yaitu,

(f o g)' (x) = f' (g (x)) . g' (x)

atau
dydx$\frac{dy}{dx}$ = dydu$\frac{dy}{du}$ . dudx$\frac{du}{dx}$

atau bisa pula dipahami sebagai,
Dxy$D_{x}y$ = Dxy$D_{x}y$

Dalam bahasa yang lebih sederhana, aturan rantai menyatakan bahwa turunan fungsi komposisi ditentukan dengan mengalikan fungsi terluar yang diturunkan terhadap fungsi di dalam (f’ (g (x)) dengan turunan dari fungsi di dalam (g’(x)). 

       Aturan ini akan lebih mudah dipahami jika kamu mempelajari contoh berikut yang diselesaikan dengan menggunakan ketiga notasi yang telah diperkenalkan sebelumnya.

Contoh

Carilah turunan pertama dari fungsi y= (x2 + x + 1)100 terhadap x.

Penyelesaian:
Untuk mempermudah perhitungan, mula-mula kita misalkan u = g (x) = x2 + x +1 sehingga diperoleh y = f (u) = u100

Adapun turunan dari kedua fungsi ini adalah u' = g' (x) = 2x +1 dan y = f' (u) = 100u99 
Dengan Notasi Lagrange:

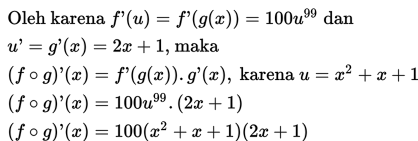
Dengan Notasi Leibniz:

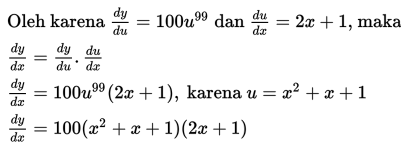
Dengan Notasi Euler: