Pada topik sebelumnya kalian telah mempelajari dan memahami topik Pertidaksamaan Kuadrat dan cara mencari Daerah Penyelesaiannya. Dalam topik ini kalian akan belajar tentang Daerah Penyelesaian Pertidaksamaan Pecahan.
Mari kita mengingat kembali bentuk Pertidaksamaan Kuadrat dan Pengertian Pecahan sebelum masuk ke topik Daerah Penyelesaian Pertidaksamaan Pecahan.
Pertidaksamaan Kuadrat
Pertidaksamaan Kuadrat adalah suatu bentuk pertidaksamaan yang memuat variabel berderajat paling tinggi dua atau berpangkat dua.
Tanda Ketaksamaan atau Pertidaksamaan yaitu > , < , ≥ , ≤
Tanda Ketaksamaan atau Pertidaksamaan yaitu > , < , ≥ , ≤
Bentuk Umum Pertidaksamaan Kuadrat
ax2 + bx + c > 0 ; ax2 + bx + c < 0 ;
ax2 + bx + c ≥ 0 ; ax2 + bx + c ≤ 0 dengan a, b, c ∈ R dan a ≠ 0
ax2 + bx + c ≥ 0 ; ax2 + bx + c ≤ 0 dengan a, b, c ∈ R dan a ≠ 0
Contoh Pertidaksamaan Kuadrat
- x2 – 4x – 5 > 0
- p2 + 2p < 3
- m2 – 16 ≥ 0
- -2x2 – 3x + 2 ≤ 0
Apakah kalian sudah ingat kembali bentuk pertidaksamaan kuadrat?
Beberapa sifat-sifat pertidaksamaan :
- Bentuk pertidaksamaan tidak berubah tanda (tetap), Jika kedua ruas dikalikan, dibagi, ditambah atau dikurangi dengan bilangan positif yang sama.
- Bentuk pertidaksamaan berubah tanda (berbalik tanda), Jika kedua ruas dikalikan atau dibagi dengan bilangan negatif.
Apakah kalian sudah ingat kembali sifat-sifat pertidaksamaan kuadrat?
Langkah-langkah menentukan daerah penyelesaian pertidaksamaan kuadrat dengan cara garis bilangan :
- Ubah pertidaksamaan dalam Bentuk Umum Pertidaksamaan Kuadrat
p2 + 2p < 3 ⇔ p2 + 2p - 3 < 0 - Menentukan pembuat nol
p2 + 2p - 3 < 0 ⇔ p2 + 2p - 3 = 0⇔ (p + 3)(p – 1) = 0⇔ p = -3 atau p = 1 - Gambar pembuat nol pada garis bilangan
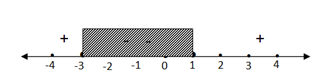
4. Tentukan Daerah Penyelesaian Pertidaksamaan kuadrat tersebut -3 ≤ x ≤ 1
Apakah kalian sudah ingat kembali langkah-langkah menentukan Daerah Penyelesaian pertidaksamaan kuadrat?
Konsep Pecahan
Mari memahami konsep pecahan melalui wacana berikut :
Pak Aditya adalah seorang guru yang sangat tekun dan sabar dalam melaksanakan pekerjaannya. Setiap hari berangkat kesekolah mengendarai sepeda motor. Jarak yang ditempuh Pak Aditya dari rumah kesekolah 32,5 km dan membutuhkan waktu 1 3/4 jam. Sekolah P Aditya memiliki siswa berjumlah 1200 anak, data siswa yang mengikuti ekstrakurikuler 35% mengikuti bola volly, 1/3 mengikuti bulu tangkis, dan sisanya mengikuti ekstra sepak bola.
Dari wacana diatas angka 32,5 ; 1 3/4 ; 35% ; 1/3 merupakan jenis-jenis bentuk pecahan.

Berbagai bentuk pecahan diatas sering kita gunakan dalam kehidupan sehari-hari untuk menjumlahkan, mengurangkan, mengalikan dan membagi.
Sifat-sifat pada bentuk pecahan
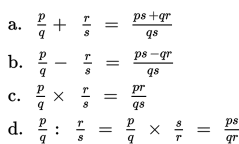
Apakah kalian sudah ingat kembali konsep pecahan dan sifat-sifatnya?
Pertidaksamaan Pecahan
Pada topik ini, kalaian akan belajar tentang pertidaksamaan pecahan dan daerah penyelesaiannya.
Pertidaksamaan pecahan mempunyai empat bentuk baku sebagai berikut :
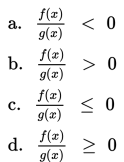
Sifat-sifat pertidaksamaan pecahan
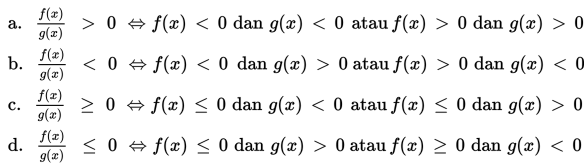
Langkah-langkah Penyelesaian pertidaksamaan pecahan adalah
- Menentukan pembuat nol pembilang dan penyebut yaitu f(x) = 0 dan g(x) = 0
- Menggambar nilai-nilai pembuat nol pada garis bilangan sehingga akan diperoleh interval-interval.
- Menentukan tanda (+) atau tanda (-) pada interval dengan cara mensubstitusikan nilai-nilai yang berada pada interval tersebut.
- Menentukan daerah penyelesaian dengan cara menentukan interval yang memenuhi pertidaksamaan pecahan tersebut.
Ingat : Bagian penyebut tidak boleh sama dengan 0 atau g(x) ≠ 0
Contoh 1 :
Tentukan daerah penyelesaian dari pertidaksamaan pecahan berikut :
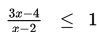
Penyelesaian :
Langkah-langkah penyelesaian :
1. Ubah soal dalam bentuk umum pertidaksamaan pecahan (ruas kanan nol)
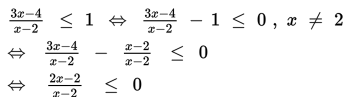
2. Tentukan nilai pembuat nol pembilang dan penyebut
Pembuat nol pembilang 2x – 2 = 0 <=> x = 1
Pembuat nol penyebut x – 2 ≠ 0 <=> x ≠ 2
Pembuat nol penyebut x – 2 ≠ 0 <=> x ≠ 2
3. Menggambar nilai-nilai pembuat nol pada garis bilangan
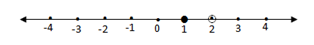
Dalam garis bilangan terdapat 3 interval : x ≤ 1, 1 ≤ x < 2, dan x > 2
Menentukan tanda (+) atau tanda (-) pada interval dengan cara mensubstitusikan nilai-nilai yang berada pada interval tersebut.
Tips :
Untuk menentukan tanda (+) atau (-) pada interval, cukup di pilih nilai dalam salah satu interval pada garis bilangan. Tanda tiap interval ditentukan oleh tanda dari inerval sebelum atau sesudahnya atau dengan pola berganti interval berganti tanda .
Pilih nilai x = 0 (interval nilai x < 1) substitusikan pada pertidaksamaan pecahan yang diketahui.

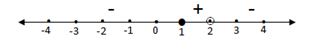
4. Menentukan daerah penyelesaian : pilih interval yang memenuhi pertidaksamaan pecahan yang diketahui dengan memperhatikan tanda pertidaksamaan pada soal (≤ 0) berarti tanda yang yang memenuhi tanda (-)
Jadi daerah penyelesaiannya adalah :
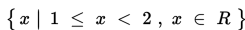
Contoh 2 :
Tentukan daerah penyelesaian dari pertidaksamaan pecahan berikut :
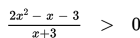
Penyelesaian :
Langkah-langkah penyelesaian :
1. Tentukan nilai pembuat nol pembilang dan penyebut
Pembuat nol pembilang
2x2 – x – 3 = 0
<=> (2x – 3)(x + 1) = 0
<=> (2x – 3) = 0 v (x + 1) = 0
<=> x = 3/2 v x = -1
Pembuat nol penyebut x + 3 ≠ 0 <=> x ≠ -3
2x2 – x – 3 = 0
<=> (2x – 3)(x + 1) = 0
<=> (2x – 3) = 0 v (x + 1) = 0
<=> x = 3/2 v x = -1
Pembuat nol penyebut x + 3 ≠ 0 <=> x ≠ -3
2. Menggambar nilai-nilai pembuat nol pada garis bilangan

Dalam garis bilangan terdapat 4 interval : x < -3, -3 < x < -1, -1 < x < 3/2 dan x > 3/2
3. Menentukan tanda (+) atau tanda (-) pada interval dengan cara mensubstitusikan nilai-nilai yang berada pada interval tersebut.
Tips :
Untuk menentukan tanda (+) atau (-) pada interval, cukup pilih nilai dalam salah satu interval pada garis bilangan. Tanda tiap interval ditentukan oleh tanda dari inerval sebelum atau sesudahnya atau dengan pola berganti interval berganti tanda .
Pilih nilai x = 0 (pada interval -1 < x < 3/2) dan substitusikan pada pertidaksamaan pecahan yang diketahui.
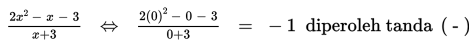
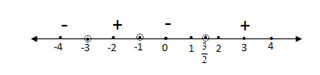
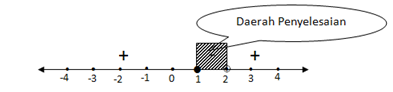
4. Menentukan daerah penyelesaian : pilih interval yang memenuhi pertidaksamaan pecahan yang diketahui dengan memperhatikan tanda pertidaksamaan pada soal ( ) berarti tanda yang yang memenuhi tanda ( + )
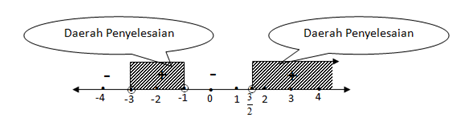
Jadi daerah penyelesaiannya adalah :
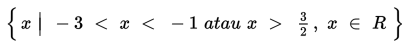
Contoh 3 :
Tentukan daerah penyelesaian dari pertidaksamaan pecahan berikut :
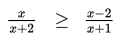
Penyelesaian :
Langkah-langkah penyelesaian :
1. Ubah soal dalam bentuk umum pertidaksamaan pecahan (ruas kanan nol)
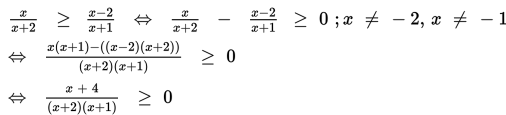
2.Tentukan nilai pembuat nol pembilang dan penyebut
Pembuat nol pembilang : x + 4 = 0 <=> x = -4
Pembuat nol penyebut :
(x + 2)(x + 1) ≠ 0 <=> x + 2 ≠ 0 v x + 1 ≠ 0 <=> x ≠ -2 v x ≠ -1
Pembuat nol penyebut :
(x + 2)(x + 1) ≠ 0 <=> x + 2 ≠ 0 v x + 1 ≠ 0 <=> x ≠ -2 v x ≠ -1
3. Menggambar nilai-nilai pembuat nol pada garis bilangan dan langsung menentukan daerah penyelesaiannya
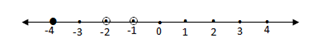
Dalam garis bilangan terdapat 4 interval : x ≤ -4, -4 ≤ x < -2,-2 < x < -1 dan x > -1
4. Langkah berikutnya bisa langsung digabung sampai diperoleh daerah penyelesaiannya.
Diawali dengan memilih nilai x = 0 (pada interval -2 < x < 1) substitusikan pada pertidaksamaan pecahan yang diketahui.
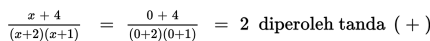

Jadi daerah penyelesaiannya adalah :
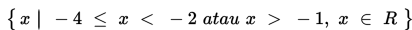
Terima kasih
ReplyDeleteSangat membantu, terusin semangatnya koo
Sama sama.. siap akan semangat
DeleteUntuk mengganti tanda tuh saat dibagi dengan negatif atau saat pembagi negatif?
ReplyDeleteSaat x nya dibagi negatif
DeleteMisak -2x > 12 terus bagi -2
Maka x < -6
Makasih atas bantuanya
ReplyDeletePusing saya gak ngerti parahhhhhhh
ReplyDelete