Dalam topik ini kalian akan mempelajari daerah penyelesaian pertidaksamaan mutlak. Sebagai persiapan awal, mari kita ingat kembali konsep-konsep dasar untuk pertidaksamaan mutlak.
Menentukan pertidaksamaan mutlak yang memenuhi daerah penyelesaian
Menentukan pertidaksamaan mutlak dari suatu grafik fungsi sama halnya dengan memperhatikan nilai pembatas pada sumbu y. Sebelum memulai lebih lanjut, mari kita perhatikan grafik fungsi y = |x| di bawah ini.

Jika grafik fungsi di atas digeser ke kanan sejauh a, maka grafik fungsi berubah menjadi
y = |x - a| dan jika grafik fungsi di atas digeser ke kiri sejauh b, maka garfik fungsi berubah menjadi y = |x + b|.
y = |x - a| dan jika grafik fungsi di atas digeser ke kiri sejauh b, maka garfik fungsi berubah menjadi y = |x + b|.
Contoh 1 :
Tentukan pertidaksamaan mutlak yang sesuai dengan daerah yang diarsir pada gambar berikut ini!
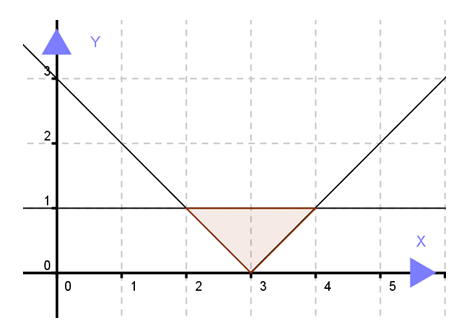
Penyelesaian :
Perhatikan bahwa grafik di atas simetri di x = 3. Dengan kata lain, grafik fungsi y = |x| bergeser ke kanan 3 satuan. Oleh karenanya, grafik fungsi menjadi
y = |x - 3|. Selanjutnya, karena daerah arsiran berada di bawah garis y = 1, maka diperoleh pertidaksamaan mutlak |x – 3| ≤ 1.
y = |x - 3|. Selanjutnya, karena daerah arsiran berada di bawah garis y = 1, maka diperoleh pertidaksamaan mutlak |x – 3| ≤ 1.
Contoh 2 :
Tentukan pertidaksamaan mutlak yang sesuai dengan daerah yang diarsir pada gambar berikut ini!
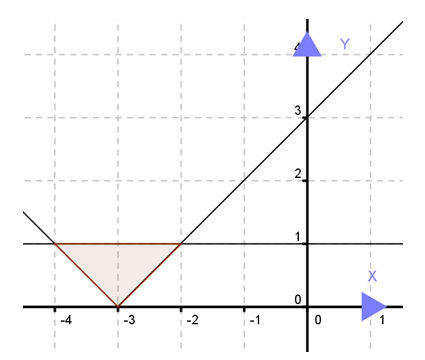
Penyelesaian :
Perhatikan bahwa grafik di atas simetri di x = -3. Dengan kata lain, grafik fungsi y = |x| bergeser ke kiri 3 satuan. Oleh karenanya, grafik fungsi menjadi y = |x + 3|. Selanjutnya, karena daerah arsiran berada di bawah garis y = 1, maka diperoleh pertidaksamaan mutlak
|x + 3| ≤ 1.
|x + 3| ≤ 1.
Menentukan Himpunan Penyelesaian Pertidaksamaan Mutlak
Mari kita ingat kembali bentuk dan cara penyelesaian pertidaksamaan mutlak.
|f(x)| < a dan a > 0
- Bentuk ini dapat diselesaikan dengan cara mengubahnya menjadi –a < f(x) < a.
|f(x)| > a dan a > 0
- Bentuk ini dapat diselesaikan dengan cara mengubahnya menjadi f(x) < -a atau f(x) > a.
|f(x)| > |g(x)|
- Bentuk ini dapat diselesaikan dengan cara mengkuadratkan kedua ruas.
Contoh 3 :
Tentukan himpunan penyelesaian dari | ½ x + 3 | < 6.
Penyelesaian :
Bentuk |½ x + 3| < 6 dapat diselesaikan dengan cara mengubahnya menjadi -6 < ½ x + 3 < 6.
Dengan demikian, diperoleh hasil sebagai berikut :
-6 - 3 < ½ x < 6 - 3
<=> - 9 < ½ x < 3
<=> -18 < x < 6
<=> - 9 < ½ x < 3
<=> -18 < x < 6
Jadi, himpunan penyelesaian dari pertidaksamaan di atas adalah {x ∈ ℝ | -18 < x < 6}.
Mas, misalnya pertidaksamaan harga mutlak ada harga mutlak lagi gimana cara ngerjainnya? Misalnya soalnya ||x|+x|>2, mohon dijawab yah boss
ReplyDelete