DEFINISI FUNGSI KOMPOSISI

Misalkan fungsi f ditentukan dengan rumus f (x) dan fungsi g ditentukan dengan rumus g (x)masing-masing terdefinisi pada daerah asalnya, maka:

• fungsi f dilanjutkan dengan fungsi g dinyatakan oleh (g o f )(x) = g (f (x)) terdefinisi jika 
  Rf ∩ Dg ≠ ∅.
• fungsi g dilanjutkan dengan fungsi f dinyatakan oleh (f o g )(x) = f (g (x)) terdefinisi jika 
  Rg ∩ Df ≠ ∅.

Dengan:

Df merupakan daerah asal fungsi f

Rf merupakan daerah hasil fungsi f

Dg merupakan daerah asal fungsi g

Rg merupakan daerah hasil fungsi g

Berdasarkan definisi tersebut, kalian dapat menentukan fungsi komposisi dari beberapa fungsi seperti contoh berikut.

Contoh 1:

Diketahui fungsi:

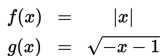
Tentukan (f o g ) (x), (g o f ) (x), dan (g o g ) (x).

Jawab:

Terlebih dahulu, tentukan daerah asal dan daerah hasil fungsi f dan g.

Daerah asal fungsi f adalah himpunan semua bilangan real, yaitu Df = R, sedangkan daerah hasilnya adalah himpunan semua bilangan real tak negatif, yaitu Rf = {y ∈ R|y ≥ 0}.

Daerah asal fungsi g adalah Dg = {x ∈ R|x ≤ -1}, sedangkan daerah hasilnya adalah 
Rg = {y ∈ R|y ≥ 0}.

• Perhatikan bahwa Rg ∩ Df ≠ ∅ sehingga (f o g) (x) terdefinisi.

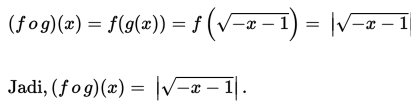
• Perhatikan bahwa Rf ∩ Dg = ∅ sehingga (g o f ) (x) tidak terdefinisi.
• Perhatikan bahwa Rg ∩ Dg = ∅ sehingga (g o g ) (x) tidak terdefinisi.

Contoh 2:

Diketahui fungsi f (x) = x + 2, g (x) = 2x – 3, dan h (x) = x2. 
Tentukan (f o (g o h))(x) dan ((f o g) o h)(x).

Jawab:

Terlebih dahulu, tentukan (g o h)(x) dan (f o g)(x).

(g o h)(x) = g (h (x)) = g (x2 ) = 2x2 – 3

Jadi, (g o h)(x) = 2x2 – 3.

(f o g)(x) = f (g(x)) = f (2x – 3) = (2x – 3) + 2 = 2x – 1

Jadi, (f o g)(x) = 2x – 1.

Sekarang, tentukan (f o (g o h))(x) dan ((f o g) o h)(x).

(f o (g o h))(x) = (f (g o h)(x)) = f (2x2 – 3) = 2x2 – 3 + 2 = 2x2 – 1

Jadi, (f o (g o h))(x) = 2x2 – 1.

Untuk menentukan ((f o g) o h)(x), misalkan (f o g)(x) = k (x). Jadi, k(x) = 2x – 1.

((f o g) ) o h)(x) = (k o h)(x) = k (h(x)) = k(x2 ) = 2x2 – 1

Jadi, ((f o g) o h)(x) = 2x2 – 1.

Dengan demikian, ((f o g) o h)(x) = (f o (g o h))(x).