Pada topik sebelumnya, kamu telah mempelajari fungsi komposisi dan fungsi invers. Tentu kamu masih ingat bukan? Pemahamanmu terhadap kedua topik tersebut dapat kamu gunakan untuk mempelajari topik berikut ini, yaitu menentukan fungsi invers dari suatu fungsi komposisi.
Misalkan h (x ) = (f o g ) (x ). Bagaimanakah cara menentukan fungsi invers h dari fungsi invers-fungsi invers komposisi fungsi penyusunnya? Perhatikan uraian berikut.
Pak Feri Abel menyuruh Cece Kigan dan Kevin Tara menentukan (f o g ) -1 (x ) dari fungsi f(x) = -3x dan g (x ) = x + 2 yang telah dituliskannya di papan tulis.

Cece Kigan mengerjakannya dengan terlebih dahulu menentukan (f o g ) (x ). Kemudian, menentukan inversnya.
(f o g ) (x ) = f (g (x )) = f (x + 2) = -3 (x + 2) = – 3x – 6
(f o g ) (x ) = – 3x – 6
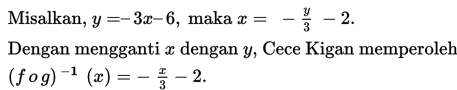
Adapun Kevin Tara mengerjakannya dengan terlebih dahulu menentukan fungsi invers dari f (x ) dan g (x ). Kemudian, menentukan fungsi komposisi dari fungsi invers tersebut, yaitu
(g -1 o f -1 ) (x ).
(g -1 o f -1 ) (x ).
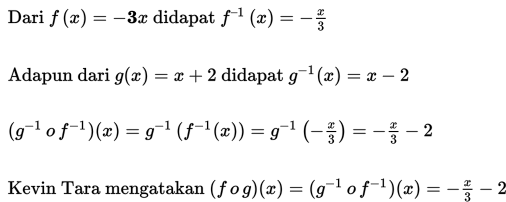
Dengan cara yang berbeda, Kevin Tara dan Cece Kigan mendapatkan jawaban yang sama. Pada akhir jawabannya, Kevin Tara mengatakan (f o g ) -1 (x ) = (g -1 o f -1 ) (x ).
Mengapa demikian?
Mengapa demikian?
Coba misalkan h (x ) = (f o g ) (x ).
Fungsi invers dari h (x ) = (f o g ) (x ) adalah h -1 (x ) = (f o g ) -1 (x ).
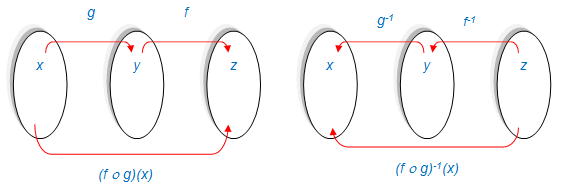
Dari gambar diagram panah tersebut, tampak bahwa (f o g ) -1 (x ) = (g -1 o f -1 ) (x ).
Dengan cara yang sama, kamu juga dapat menunjukkan bahwa:
(g o f ) -1 (x ) = (f -1 o g -1 ) (x ).
Uraian tersebut menggambarkan hubungan berikut.
Jika f (x ) dan g (x ) fungsi bijektif dan f -1 (x ) dan g -1 (x ) masing-masing merupakan fungsi inversnya maka (f o g ) -1 (x ) = (g -1 o f -1 ) (x ) dan (g o f ) -1 (x ) = (f -1 o g -1 ) (x ).
Contoh:
Diketahui fungsi f (x ) = 2 – x dan g (x ) = – 2x. Tentukanlah:
1. (f o g ) (x ) dan (g o f ) (x )
2. (f o g ) -1 (x ) dan (g o f ) -1 (x ) dari hasil jawaban 1
3. f -1 (x ) dan g -1 (x )
4. (f o g ) -1 (x ) dan (g o f ) -1 (x ) dari hasil jawaban 3
Penyelesaian:
1. (f o g ) (x ) = f (g (x )) = f (–2x ) = 2 – (-2x ) = 2 + 2x
(g o f ) (x ) = g (f (x )) = g (2 – x ) = – 2(2 – x) = -4 + 2x
Jadi, (f o g ) (x ) = 2 + 2x dan (g o f ) (x ) = -4 + 2x.
2. (f o g ) (x ) = 2 + 2x
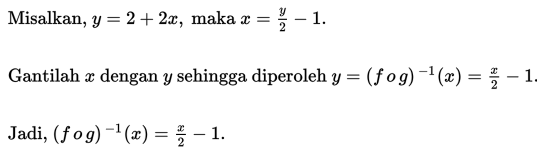
(g o f ) (x ) = -4 + 2x.

3. f (x ) = 2 – x, berarti
f -1 (x ) = 2 – x
g (x ) = –2x, berarti
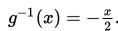
4. (f o g ) -1 (x ) = (g -1 o f -1 ) (x ) = g -1 (f -1 (x )) dengan demikian, diperoleh:
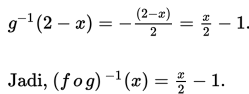
(g o f ) -1 (x ) = (f -1 o g -1 ) (x ) = f -1 (g -1 (x )) dengan demikian, diperoleh:
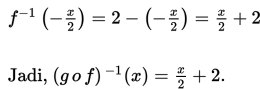
0 komentar:
Post a Comment