KEDUDUKAN TITIK, GARIS, DAN BIDANG DALAM RUANG TIGA DIMENSI

Kedududukan titik dan garis dalam ruang

Sebuah titik dapat terletak pada suatu garis atau berada di luar suatu garis.

• Titik A dikatakan terletak pada garis g jika titik A dilalui oleh garis g.

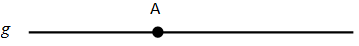
• Titik A dikatakan berada di luar garis g jika titik A tidak dilalui oleh garis g.

Cukup mudah dipahami bukan?

Kedudukan titik dan bidang dalam ruang

Sama halnya dengan kedudukaan titik terhadap garis, sebuah titik dapat terletak pada bidang atau berada di luar bidang.

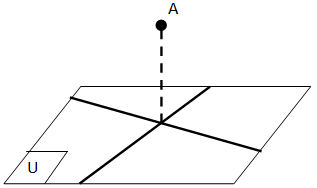
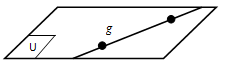
• Titik A dikatakan terletak pada bidang U, jika titik A dilalui oleh bidang U

• Titik A dikatakan berada di luar bidang U jika titik A tidak dilalui oleh bidang U

Kedudukan antara dua garis dalam ruang

Dua buah garis dalam ruang dapat saling berimpit, sejajar, berpotongan, atau bersilangan.
Agar lebih jelas, mari kita cermati beberapa definisi di bawah ini.

• Garis g dikatakan berimpit dengan garis h jika setiap titik pada garis g terletak pada garish.

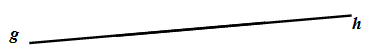
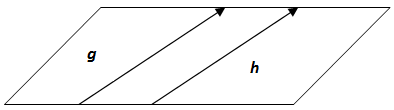
• Garis g dikatakan sejajar dengan garis h jika kedua garis tersebut tidak mempunyai titik persekutuan dan sebidang

• Garis g dan garis h akan berpotongan jika garis g dan h mempunyai tepat satu titik persekutuan dan sebidang.

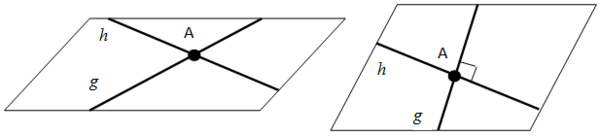
• Garis g dan garis h bersilangan. jika kedua garis tersebut tidak mempunyai titik persekutuan dan tidak terletak dalam satu bidang.

Kedudukan garis dan bidang dalam ruang

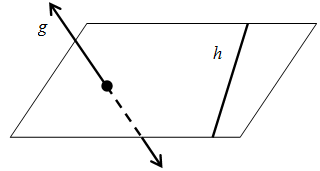
Sebuah garis dapat memotong bidang, sejajar dengan bidang, atau menembus bidang.
Yuk kita cermati beberapa ilustrasi di bawah ini.

• Sebuah garis dikatakan berpotongan dengan bidang jika garis dan bidang tersebut mempunyai paling sedikit dua titik persekutuan.

• Sebuah garis dikatakan sejajar dengan bidang jika tidak ada titik persekutuan atau garis tersebut sejajar dengan salah satu garis yang terletak pada bidang tersebut. Pada ilustrasi di bawah, garis g dikatakan sejajar bidang U karena garis g sejajar dengan salah satu garis yang terletak pada bidang U.

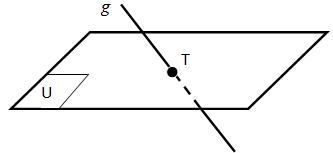
• Sebuah garis dikatakan memotong/menembus bidang jika mempunyai 1 titik persekutuan. Pada ilustrasi di bawah, garis g menembus bidang U dengan titik potong adalah titik T.

Kedudukan dua bidang dalam ruang

Dua buah bidang dapat dikatakan berimpit, sejajar, dan berpotongan.

Agar lebih jelas, mari kita cermati beberapa definisi berikut.

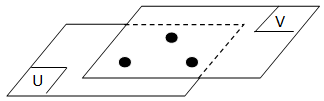
• Dua bidang dikatakan berimpit jika mempunyai tiga titik tidak segaris yang merupakan titik persekutuan. Dalam ilustrasi di bawah ini, bidang U berimpit dengan bidang V.

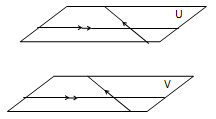
• Dua bidang dikatakan sejajar jika tidak mempunyai titik persekutuan. Dalam ilustrasi di bawah ini, bidang U sejajar dengan bidang V

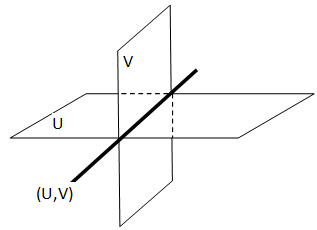
• Dua bidang berpotongan jika mempunyai tepat satu garis persekutuan. Dalam ilustrasi di bawah ini, bidang U memotong bidang V dengan garis potong (U, V).