MANIPULASI ALJABAR DALAM MENYELESAIKAN MASALAH MATEMATIKA PERTIDAKSAMAAN PECAHAN

Dalam topik ini kalian akan belajar mengenai manipulasi aljabar dalam pertidaksamaan pecahan. Sebelumya, kalian pasti telah belajar dan mengetahui tentang berbagai bentuk pertidaksamaan linear. Mari kita mulai belajar. Tetap semangat!!!

1. Pertidaksamaan Pecahan
Pertidaksamaan pecahan adalah pertidaksamaan yang melibatkan persamaan pembilang dan penyebut dengan tanda pertidaksamaan (<, ≤, >, ≥).

Contoh pertidaksamaan pecahan, yaitu

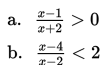
Bentuk baku dari pertidaksamaan bentuk pecahan, yaitu:

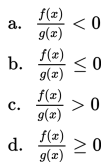
dengan syarat g(x) ≠ 0.

2. Langkah-Langkah Menyelesaikan Pertidaksamaan Pecahan

Langkah-langkah menyelesaikan pertidaksamaan pecahan :
a. Ubahlah pertidaksamaan yang ada sehingga salah satu ruas adalah nol
b. Samakan penyebutnya
c. Menentukan pembuat nol ruas yang memuatvariabel.
d. Menuliskan nilai – nilai tersebut pada garis bilangan.
e. Uji interval.

Contoh 1
Tentukan himpunan penyelesaian pertidaksamaan

Penyelesaian:

a. Ubahlah pertidaksamaan yang ada sehingga salah satu ruas adalah nol

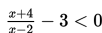
b. Menyederhanakan ruas kiri (samakan penyebutnya).

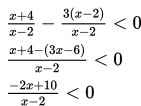
c. Menentukan pembuat nol ruas kiri.
-2x + 10 = 0
x = 5
dan
x – 2 = 0
x = 2

d. Menuliskan nilai – nilai tersebut pada garis bilangan.

Catatan: Biarkan titik tidak diarsir, tergantung tanda pertidaksamaan dan hasil uji interval.

e. Uji interval.
Subsitusikan x = 0 ke (b) yaitu

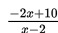
sehingga diperoleh nilai 10/-2 = -5 (nilai negatif). Jadi daerah yang diarsir adalah

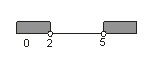
Catatan: Nilai negatif untuk tanda (<, ≤). Nilai positif untuk tanda (>, ≥).
Himpunan penyelesaian: { x | x < 2 atau x > 5 }

Contoh 2
Tentukan himpunan penyelesaian pertidaksamaan

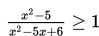
Penyelesaian:

a. Ubahlah pertidaksamaan yang ada sehingga salah satu ruas adalah nol

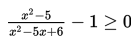
b. Menyederhanakan ruas kiri (samakan penyebutnya).

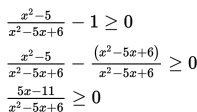
c. Memfaktorkan ruas kiri

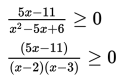
d. Menentukan pembuat nol ruas kiri.
5x – 11 = 0
x = 11/5
dan
x – 2 = 0
x = 2
dan
x – 3 = 0
x = 3

e. Menuliskan nilai – nilai tersebut pada garis bilangan.

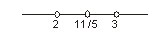
Catatan: Biarkan titik tidak diarsir, tergantung tanda pertidaksamaan dan hasil uji interval.

f. Uji interval.
Subsitusikan x = 0 ke (b) yaitu

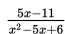
sehingga diperoleh nilai -11/6 (nilai negatif).

Jadi daerah yang diarsir adalah

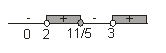
Perhatikan bahwa hanya titik 11/5 yang hitam diarsir, karena tanda pertidaksamaan (≥), sedangkan titik 2 dan 3 tidak diarsir karena berperan sebagai penyebut.
Catatan: Nilai negatif untuk tanda (<, ≤). Nilai positif untuk tanda (>, ≥).

Perhatikan bahwa jika tidak memuat akar kembar maka tanda akan selalu bergantian, yaitu

Himpunan penyelesaian: { x | 2 < x ≤ 11/5 atau x > 3 }