Dalam topik ini kalian akan belajar tentang manipulasi aljabar dalam menyelesaikan pertidaksamaan irrasional. Mari kita mulai mempelajari topik ini.
- Pertidaksamaan Irrasional Pertidaksamaan bentuk akar atau lebih dikenal dengan nama pertidaksamaan irrasional adalah pertidaksamaan yang bentuk aljabarnya melibatkan tanda akar. Agar adik-adik lebih jelas dan lebih memahami, mari kita perhatikan bentuk-bentuk berikut ini.

Bentuk-bentuk di atas merupakan contah pertidaksamaan irrasional karena mengandung bentuk aljabar yang melibatkan tanda akar.
Adapun bentuk pertidaksamaan irrasional adalah:
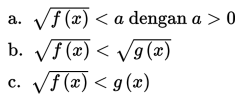
Catatan: bentuk-bentuk di atas juga berlaku untuk tanda pertidaksamaan (<, >, ≤, ≥)
- Langkah-Langkah Menyelesaikan Pertidaksamaan Irrasional
Perhatikan bentuk-bentuk pertidaksamaan Irrasional
a. Bentuk
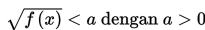
Mari adik-adik cermati. Pertidaksamaan ini akan lebih mudah dikerjakan jika kita hilangkan tanda akar dengan mengkuadratkan kedua ruas. Selain itu, ingat bahwa f(x) di dalam akar pasti bernilai non negatif.
Secara umum langkah yang digunakan untuk memperoleh penyelesaiannya adalah
1. f(x) < a2
2. f(x) ≥ 0
1. f(x) < a2
2. f(x) ≥ 0
Contoh:
Tentukan himpunan penyelesaian dari
Tentukan himpunan penyelesaian dari
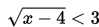
Penyelesaian:
- (x – 4) < 32
Selanjutnya, adik-adik bisa memanipulasi bentuk aljabarnya menjadi
(x – 4) < 9
x < 9 + 4
x < 13 - (x – 4) ≥ 0
Dari fakta ini, diperoleh x ≥ 4.
Diperoleh daerah penyelesaian
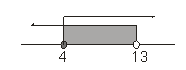
Himpunan penyelesaian adalah {x | 4 ≤ x < 13}
b. Bentuk
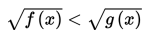
Jika adik-adik telah memahami materi sebelumnya, maka bagian ini akan sangat mudah dipahami. Perbedaannya adalah bahwa pada bagian ini ada 2 suku yang berada di bawah tanda akar.
Secara umum, bentuk ini dapat diselesaikan dengan cara:
- f(x) < g(x)
- f(x) ≥ 0
- g(x) ≥ 0
Contoh:
Tentukan himpunan penyelesaian dari
Tentukan himpunan penyelesaian dari
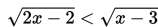
Penyelesaian:
- 2x – 2 < x – 3
Dengan menggunakan manipulasi aljabar, diperoleh
2x – x < -3 + 2
x < -1 - 2x – 2 ≥ 0
Dengan menggunakan manipulasi aljabar, diperoleh
2x ≥ 2
x ≥ 1 - x – 3 ≥ 0
Selanjutnya, diperoleh x ≥ 3
Diperoleh daerah penyelesaian
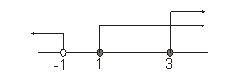
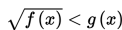
Himpunan penyelesaian: { } atau Ø, karena ketiga daerah tidak beririsan.
c. Bentuk
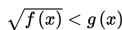
Bentuk ini sebenarnya tidak terlalu berbeda dengan bentuk a) dan b), sehingga teknik penyelesaiannya juga sama.
Adapun cara menyelesaikannya:
1. f(x) < (g(x))2
2. f(x) ≥ 0
3. g(x) ≥ 0
1. f(x) < (g(x))2
2. f(x) ≥ 0
3. g(x) ≥ 0
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan
Tentukan himpunan penyelesaian dari pertidaksamaan
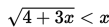
Penyelesaian:
- 4 + 3x < x2
Dengan manipulasi aljabar, diperoleh
4 + 3x < x2
-x2 + 3x + 4 < 0
-x2 + 3x + 4 < 0
Dengan menggunakan sifat perkalian bilangan negatif, maka tanda persamaan berubah menjadi
x2 – 3x – 4 > 0
(x – 4)(x + 1) > 0
x2 – 3x – 4 > 0
(x – 4)(x + 1) > 0
Titik pembuat nol x = 4 dan x = -1.
Daerah penyelesaian
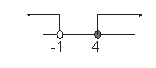
- 4 + 3x ≥ 0
Dengan manipulasi sifat aljabar, diperoleh x ≥ -4/3 - x ≥ 0
Diperoleh daerah penyelesaian

Daerah penyelesaian adalah irisan ketiga daerah yang disyaratkan.Untuk -4/3 ≤ x < -1 bukan merupakan daerah penyelesaian karena hanya merupakan irisan dua daerah yang disyaratkan.
Jadi, himpunan penyelesaian adalah {x | x > 4}.
0 komentar:
Post a Comment