Menggunakan definisi geometris II
Rotasi
Karena rotasi adalah gerakan yang melalui busur lingkaran, dapat kita misalkan pusat of rotasi,( pusat lingkaran) adalah O(x,y) dan titik yang dirotasikan adalah P(h,k) maka
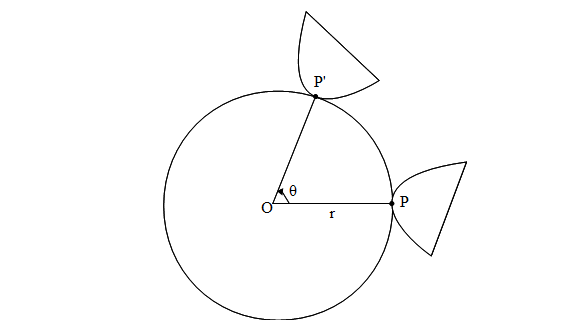
- Jarak bayangan ke titik pusat = Jarak objek ke titik pusat, besarnya adalah panjang ruas garis OP.
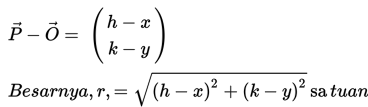
- Jika objek P bergerak dari titik P ke titik P' sebesar sudut tertentu, theta, maka besar perpindahannya sama dengan panjang busur PP' yangjari-jarinya r seperti pada persamaan di atas. Kita ambil nilai mutlak dari theta karena thetanilainya bisa positif ataupun negatif.Panjang busur adalah pecahan darikeliling lingkaran dan dapat diperoleh dengan cara seperti berikut ini
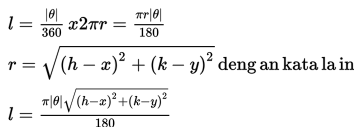
- Luas area yang dibentuk oleh pergerakan objek, r, adalah luas dari bidang PP'O yang mana merupakan bagian dari luas lingkaran. Dapat ditulis
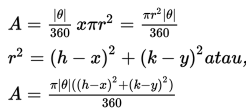
Refleksi
Perhatikan objek A(x,y) dipetakan ke A'(x',y') dengan garis PQ sebagai cermin.
1. Karena jarak objek ke cermin = jarak bayangan ke cermin, titik potong M adalah
titik tengah dari garis AA' seperti berikut ini
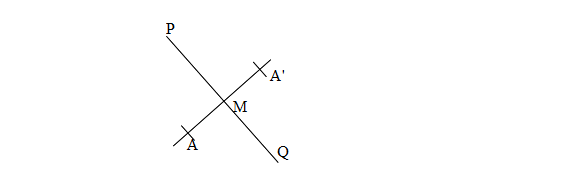

Jarak terpendek antara bayangan dengan garis cermin sama dengan jarak terpendek antara objek dengan garis cermin. Jarak ini sama dengan AM = A'M. Dapat ditulis seperti berikut ini
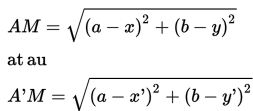
Ambil persamaan pertama, kita peroleh
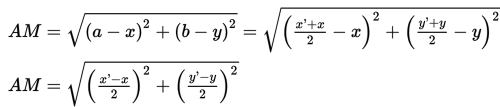
Jarak antara dua titik (objek dan bayangan) adalah 2AM, atau
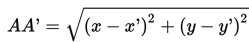
Translasi
Pada saat sebuah titik ditranslasikan dari P(x,y) ke P'(x,y), vektor yang mendeskripsikan hal itu disebut vektor translasi .
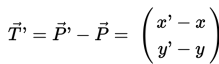
Ketika diberikan vektor translasi dan koordinat objek yang akan ditranslasikan, bayangannya dapat diperoleh dengan cara sebagai berikut
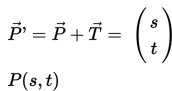
Besarnya perpindahan objek translasi adalah jarak pergeseran titik P ke P', yaitu
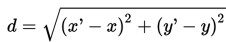
Tapi jarak pergeseran sama dengan modulus vektor translasi T. Dengan demikian jaraknya, d, yang merupakan besar dari perpindahan objek yang ditranslasikan, adalah modulus dari vektor translasi, T. Thus
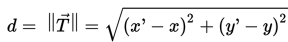
0 komentar:
Post a Comment