Pada topik sebelumnya kita telah mempelajari konsep pertidaksamaan kuadrat dua variabel. Dalam topik ini kita akan mempelajari model matematika sistem pertidaksamaan kuadrat dua variabel.
Sebelum kita memulai topik model matematika sistem pertidaksamaan kuadrat dua variabel, marilah kita mengingat kembali konsep dari sistem pertidaksamaan kuadrat dua variabel.
Sebelum kita memulai topik model matematika sistem pertidaksamaan kuadrat dua variabel, marilah kita mengingat kembali konsep dari sistem pertidaksamaan kuadrat dua variabel.
Sistem Pertidaksamaan kuadrat dua variabel
Pertidaksamaan kuadrat dua variabel merupakan pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi dua.
Contoh bentuk umum pertidaksamaan kaudrat dua variabel
Pertidaksamaan kuadrat dua variabel merupakan pertidaksamaan yang memuat dua variabel dengan pangkat tertinggi dua.
Contoh bentuk umum pertidaksamaan kaudrat dua variabel
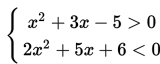
Apakah kalian sudah ingat kembali? Jika sudah, mari kita pelajari model matematika sistem Pertidaksamaan kuadrat dua variabel
Model Matematika Sistem Pertidaksamaan Kuadrat Dua Variabel
Langkah – langkah dalam menyelesaikan model matematika sistem pertidaksamaan kuadrat dua variabel yaitu :
1. Mencari kata – kata seperti “ kurang dari”(<), “lebih dari”(>), “tidak lebih dari”(≤), tidak kurang dari”(≥).
2. Setelah menemukan kata – kata tersebut merumuskan model matematika dari masalah
3. Menentukan penyelesaian dari model matematika
4. Memberikan penafsiran dari hasil yang didapat
Agar lebih memahami marilah kita mencermati contoh dibawah ini
Contoh:
Panjang dan lebar dari persegi panjang ABCD masing – masing 30 cm dan 20 cm bagian tepi persegi panjang tersebut dipotong selebar x2 sehingga diperoleh persegi panjang PQRS. Jika keliling persegi panjang PQRS tidak kurang dari 52 cm maka tentukan batas – batas x yang dapat dilakukan.
Penyelesaian:
Misal panjang persegi panjang PQRS = 30- 2x2 , lebar persegi panjang PQRS = 20 – 2x2
Keliling persegi panjang PQRS ≤ 52
2( p + l) ≤ 52
2(30 – 2x2 + 20 -2x2 ) ≤ 52
2( 50 – 4x2 ) ≤ 52
100 – 8x2 ≤ 52
-8x2 ≤ 52 -100
8x2 ≥ 48
x2 ≥ 6
1. Mencari kata – kata seperti “ kurang dari”(<), “lebih dari”(>), “tidak lebih dari”(≤), tidak kurang dari”(≥).
2. Setelah menemukan kata – kata tersebut merumuskan model matematika dari masalah
3. Menentukan penyelesaian dari model matematika
4. Memberikan penafsiran dari hasil yang didapat
Agar lebih memahami marilah kita mencermati contoh dibawah ini
Contoh:
Panjang dan lebar dari persegi panjang ABCD masing – masing 30 cm dan 20 cm bagian tepi persegi panjang tersebut dipotong selebar x2 sehingga diperoleh persegi panjang PQRS. Jika keliling persegi panjang PQRS tidak kurang dari 52 cm maka tentukan batas – batas x yang dapat dilakukan.
Penyelesaian:
Misal panjang persegi panjang PQRS = 30- 2x2 , lebar persegi panjang PQRS = 20 – 2x2
Keliling persegi panjang PQRS ≤ 52
2( p + l) ≤ 52
2(30 – 2x2 + 20 -2x2 ) ≤ 52
2( 50 – 4x2 ) ≤ 52
100 – 8x2 ≤ 52
-8x2 ≤ 52 -100
8x2 ≥ 48
x2 ≥ 6
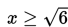
Panjang persegi panjang PQRS ≥ 0
30 – 2x2 ≥ 0
-2x2 ≥ - 30
2x2 ≤ 30
x2 ≤ 15
30 – 2x2 ≥ 0
-2x2 ≥ - 30
2x2 ≤ 30
x2 ≤ 15
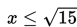
Batas – batas yang dapat dilakukan
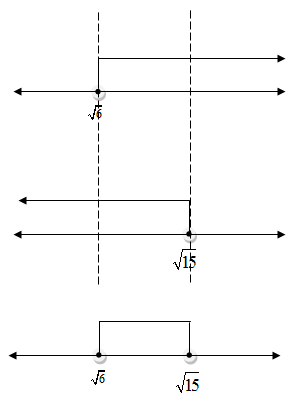
0 komentar:
Post a Comment