Pada topik sebelumnya, kalian telah mempelajari pengertian dan nilai dari suku banyak. Tentu kalian sudah paham bukan? Nah, bagaimana dengan pembagian pada suku banyak? Apakah kalian telah memahaminya? Wajar saja kalau kalian belum paham karena materi tersebut baru akan kalian pelajari pada topik kali ini.
Operasi pembagian suku banyak yang akan kalian pelajari adalah pembagian suku banyak oleh bentuk linear dan oleh bentuk kuadrat. Pada topik ini, akan dijelaskan secara detail mengenai operasi pembagian suku banyak oleh bentuk linear. Untuk pembagian suku banyak oleh bentuk kuadrat akan kalian pelajari pada topik selanjutnya.
Mari kita mulai dengan meninjau apa yang terjadi jika suku banyak P (x) dibagi dengan bentuk-bentuk linear bervariabel tunggal (x - k) atau (ax + b). Untuk mengetahui apa yang akan terjadi, kalian harus memahami cara pembagian suku banyak oleh bentuk linear. Ada dua cara yang bisa digunakan, yaitu metode pembagian bersusun dan metode skema. Mari kita pelajari satu persatu dengan penuh rasa ingin tahu.
Metode Pembagian Bersusun
Kalian tentu sudah sangat mahir melakukan pembagian suatu bilangan dengan metode bersusun bukan? Metode tersebut sudah sangat sering kalian gunakan ketika duduk di bangku SD. Tahukah kalian kalau metode tersebut dapat digunakan dalam membahas konsep pembagian suku banyak? Mari perhatikan penjelasan berikut ini.
Misalkan untuk menghitung 16 : 3, dengan menggunakan metode pembagian bersusun, diperoleh:
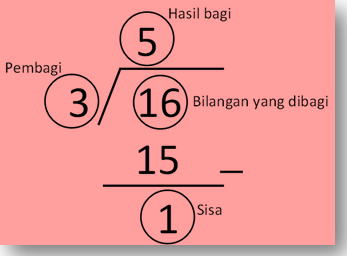
Dapat dituliskan:
16 = (3 x 5) + 1
Bilangan yang dibagi = (Pembagi x Hasil bagi) + Sisa
Sekarang, konsep tersebut mari kita terapkan pada pembagian suku banyak.
Perhatikan contoh berikut ini.
Pembagian Bersusun oleh Bentuk Linear (x - k)
Contoh
Hasil dan sisa pembagian dari suku banyak
P (x) = 2x 4 + 3x 3 - 4x 2 + x + 15 oleh bentuk linear q (x) = x - 3
adalah ....
Penyelesaian:
Pahami langkah-langkah penyelesaian berikut ini.
Langkah 1
Menuliskan suku banyak yang dibagi P (x) dan pembaginya q (x) kedalam notasi pembagian bersusun.
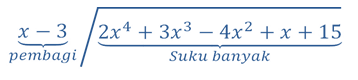
Langkah 2
Menentukan suatu suku yang apabila dikalikan dengan suku berderajat tertinggi pada pembagi q (x) akan menghasilkan suku dengan derajat tertinggi pada suku banyak yang dibagi P (x).
Pada kasus ini, 2x 3 merupakan suku yang dimaksud karena 2x 3 . x = 2x 4. Tuliskan hasil perkalian 2x 3 dengan pembagi (x - 3) dibawah suku banyak yang dibagi P (x).
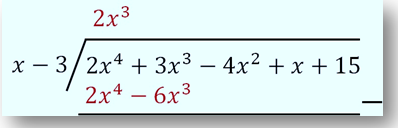
Langkah 3
Mengurangkan P (x) dengan hasil dari langkah 2.
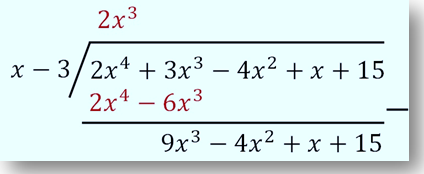
Langkah 4
Mengulang langkah 2 dan 3 hingga pembagian tidak lagi dapat dijalankan.
Pada akhir proses ini akan diperoleh pembagian bersusun sebagai berikut.
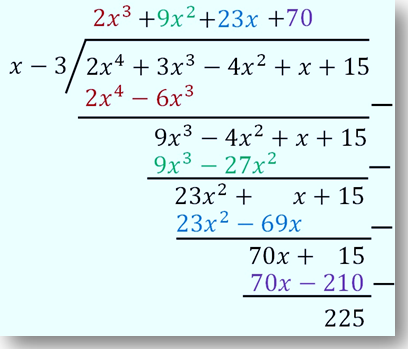
Melalui perhitungan tersebut, dapat disimpulkan:
hasil bagi = 2x 3 + 9x 2 + 23x + 70
sisa = 225
Jadi, P (x) = (x - 3) (2x 3 + 9x 2 + 23x + 70) + 225.
Pembagian Bersusun oleh Bentuk Linear (ax + b)
Contoh
Hasil dan sisa pembagian dari suku banyak
P (x) = 2x 4 + 3x 3 - 4x 2 + x + 15 oleh bentuk linear q (x) = 2x + 3
adalah ....
Penyelesaian:
Mari kita gunakan langkah yang sama seperti pada pembagian oleh bentuk (x - k), diperoleh:
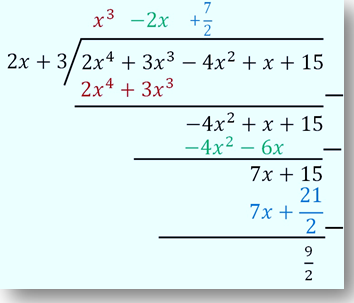
Dengan demikian,
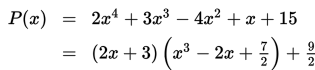
Apakah kalian sudah paham cara pembagian suku banyak dengan metode pembagian bersusun? Tentu sudah bukan? Sekarang, mari kita belajar tentang pembagian suku banyak dengan metode skema. Mari kita simak bersama-sama.
Metode Skema (Metode Horner)
Pada topik sebelumnya, kalian telah belajar menggunakan metode skema untuk menentukan nilai suku banyak. Sekarang, mari kita gunakan metode tersebut untuk menentukan hasil bagi dan sisanya.
Metode Horner oleh Bentuk Linear (x - k)
Pembagian oleh bentuk linear ini dapat ditulis sebagai P (x) = (x - k) H (x) + S dengan
P (x) adalah suku banyak yang dibagi, (x - k) adalah pembagi bentuk linear, H (x) adalah hasil bagi, dan S adalah sisa pembagiannya. Agar kalian dapat memahami dengan baik, perhatikan contoh berikut ini.
P (x) adalah suku banyak yang dibagi, (x - k) adalah pembagi bentuk linear, H (x) adalah hasil bagi, dan S adalah sisa pembagiannya. Agar kalian dapat memahami dengan baik, perhatikan contoh berikut ini.
Contoh
Hasil dan sisa pembagian dari suku banyak
P (x) = 4x 4 + 2x 2 + 2x - 16 oleh bentuk linear q (x) = x + 2
adalah ....
Penyelesaian:
Perhatikan langkah-langkah berikut ini.
Langkah 1
Melengkapi bentuk suku banyak P (x), karena suku x 3 tidak muncul didalam suku banyak ini.
P (x) = 4x 4 + 0x 3 + 2x 2 + 2x - 16
Adapun koefisien lengkap dari suku banyak ini adalah 4, 0, 2, 2, -16.
Langkah 2
Mencari pembuat nol dari pembagi q (x).
q (x) = 0
x + 2 = 0
x = -2
Jadi, -2 adalah pembuat nol dari pembagi.
Langkah 3
Menghitung nilai suku banyak menggunakan bantuan skema untuk menentukan hasil bagi dan sisanya.
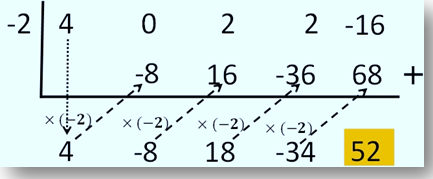
Pada baris terakhir skema, bilangan paling kanan (52) merupakan sisa pembagian sedangkan bilangan lainnya pada baris yang sama (4, -8, 18, dan -34) merupakan koefisien dari hasil bagi, sehingga didapatkan:
hasil bagi = 4x 3 - 8x 2 + 18x - 34
sisa = 52
Jadi, P (x) = (x + 2) (4x 3 - 8x 2 + 18x - 34) + 52
Metode Horner oleh Bentuk Linear (ax + b)
Cara yang digunakan untuk menetukan hasil bagi dan sisa pembagian oleh bentuk ini sebenarnya hampir sama dengan pembagian oleh bentuk sebelumnya. Hanya saja ada beberapa hal yang perlu kalian perhatikan.

Contoh
Hasil dan sisa pembagian dari suku banyak
P (x) = 2x 2 + 5x + 7 oleh bentuk linear q (x) = 2x + 1
adalah ....
Penyelesaian:
Suku banyak ini merupakan suku banyak bersuku lengkap, dengan koefisien lengkapnya 2, 5,dan 7. Adapun pembuat nol dari pembagi q (x) = 2x + 1 ditentukan sebagai berikut:
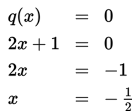
Dengan informasi tersebut kalian dapat menyusun bagan atau skema seperti berikut.
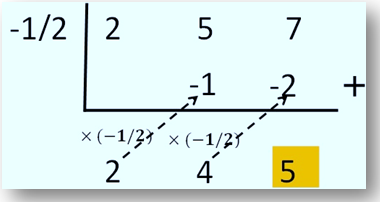
Apakah kalian sudah bisa menuliskan hasil bagi dan sisa dari pembagian suku banyak ini? Ingat bahwa (2x + 4) pada bagan diatas bukan hasil sebenarnya, karena pembagian suku banyak oleh bentuk linear (ax + b) mempunyai hasil bagi yang dibagi lagi dengan penyebut pembaginya. Coba kalian cermati kembali penjelasan tentang pembagian suku banyak oleh bentuk (ax + b) .
Jadi, hasil bagi dan sisanya adalah:

0 komentar:
Post a Comment