PENERAPAN PENERAPAN PERTIDAKSAMAAN IRRASIONAL PADA KEHIDUPAN SEHARI-HARI

Dalam topik ini kalian akan belajar mengenai penerapan pertidaksamaan irasional pada masalah nyata.

Pertidaksamaan irrasional adalah pertidaksamaan yang variabelnya terletak di bawah tanda akar.

Ada dua bentuk umum pertidaksamaan bentuk akar, yaitu :

Dalam menyelesaikan pertidaksamaan irasional terdapat syarat tambahan selain ketentuan umum, yaitu :

• Bentuk bilangan yang berada di bawah tanda akar adalah ≥ 0.

Misalnya: pada √(x – 2), harus berlaku x – 2 ≥ 0.

• Bilangan bilangan hasil penarikan akar adalah ≥ 0.

Mari kita cermati beberapa contoh soal berikut ini.

Contoh 1 :

Perusahaan asuransi melakukan perhitungan premi yang akan dibayarkan kepada pemegang polis dalam kurun waktu tertentu. Besar premi yang akan dibayarkan memenuhi persamaan berikut :

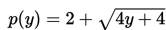
Tentukan batas kurun waktu y (dalam bulan) yang diperlukan oleh pemegang polis agar mendapat premi paling banyak 6 unit!

Penyelesaian :

Agar pemegang polis mendapat premi paling banyak 6 unit, maka p(y) haruslah kurang dari atau sama dengan enam.

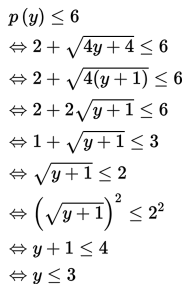
Syarat tambahan : y + 1 ≥ 0 <=> y ≥ -1

Dengan demikian. himpunan penyelesaian dari pertidaksamaan di atas adalah { -1 ≤ y ≤ 3 }.

Jadi, batas kurun waktu yang diperlukan oleh pemegang polis agar mendapat premi paling banyak 6 unit adalah 0 sampai 3 bulan.

Contoh 2 :

Pak Hasrul, guru bimbingan konseling sedang membuat laporan berupa grafik tingkat ketidakhadiran siswa selama satu bulan proses belajar berlangsung. Pak Hasrul dihadapkan dengan dua kurva yang akan digambarkan pada kertas milimeter.

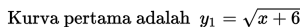
dan kurva kedua adalah y2 = x. Tentukan batas-batas nilai x yang dibutuhkan Pak Hasrul dalam menyelesaikan perhitungan jika disyaratkan kurva y1 harus selalu berada di bawah kurva y2!

Penyelesaian :

Agar kurva y1 selalu berada di bawah kurva y2, maka y1 haruslah lebih kecil dari y2.

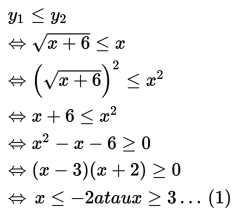
Syarat tambahan : x + 6 ≥ 0 <=> x ≥ -6 ……. (2)

Irisan dari (1) dan (2) merupakan himpunan penyelesaian pertidaksamaan di atas. Dengan demikian, himpunan penyelesaiannya adalah { -6 ≤ x ≤ -2 atau x ≥ 3 }.

Contoh 3 :

Sebuah sepeda melaju di jalan raya selama t detik dengan panjang lintasan (dalam meter) ditentukan oleh persamaan berikut :

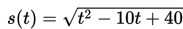
Jika panjang lintasan sepeda sekurang-kurangnya adalah 4 meter, tentukan nilai t yang memenuhi!

Penyelesaian :

Oleh karena panjang lintasan sepeda sekurang-kurangnya adalah 4 meter, maka s(t) haruslah lebih besar atau sama dengan empat.

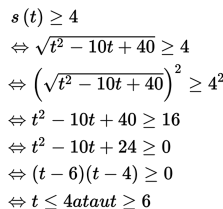
Syarat tambahan :

t2 – 10t + 40 ≥ 0 → selalu terpenuhi, karena t2 – 10t + 40 definit positif (a > 0 dan D < 0).

Dengan demikian, nilai t yang memenuhi adalah t ≤ 4 detik atau t ≥ 6 detik.