PENERAPAN PERTIDAKANSAMAAN PECAHAN PADA MASALAH KEHIDUPAN SEHARI-HARI

Sebelum mempelajari topik ini, terlebih dahulu marilah kita mengingat kembali materi pertidaksamaan pecahan. Pertidaksamaan pecahan adalah pertidaksamaan yang mempunyai bentuk pecahan dan mengandung suatu variabel (misal x) pada penyebutnya.

Pertidaksamaan Pecahan Bentuk Linear

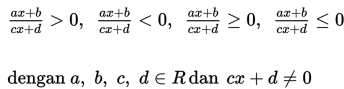
Pertidaksamaan Pecahan Bentuk Kuadrat

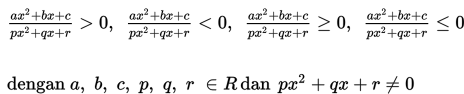
Kedua bentuk pertidaksamaan pecahan di atas dapat diselesaikan dengan cara sebagai berikut :

1. Tempatkanlah pembuat nol yang diperoleh dari pembilang dan penyebut pada suatu garis bilangan.
2. Periksa tanda dari nilai pecahan ini pada tiap interval yang terbentuk.
3. Tentukan himpunan penyelesaian sesuai dengan tanda pertidaksamaannya.

Agar kalian lebih memahami materi ini, mari kita cermati beberapa contoh soal berikut ini.

Contoh 1:

Pak Ahmed sedang mendesain animasi gambar yang melibatkan dua kurva berikut :

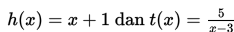
Pak Ahmed menginginkan letak kurva h(x) di atas kurva t(x). Tentukan batas-batas nilai x yang dibutuhkan Pak Ahmed untuk mendesain gambar tersebut!

Penyelesaian :

Agar kurva h(x) di atas kurva t(x) maka nilai h(x) haruslah lebih besar dari t(x).

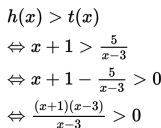
Pembuat nol pembilang :
(x + 1)(x – 3) = 0 <=> x = -1 atau x = 3

Pembuat nol penyebut :
x – 3 = 0 <=> x = 3

Jadi, batas-batas nilai x yang dibutuhkan Pak Ahmed untuk mendesain animasi gambar adalah {x ∈ ℝ| -1 < x < 3}.

Contoh 2:

Sebuah parabola dengan persamaan (p – 2)x2 + 2px + p – 1 = 0 memiliki dua akar, yaitu mdan n. Jika jumlah kedua akar lebih kecil dari nol, berapakah batas-batas nilai p yang memenuhi?

Penyelesaian :

Persamaan parabola (p – 2)x2 + 2px + p – 1 = 0 merupakan persamaan kuadrat dengan 
a = p – 2, b = 2, c = p – 1.

Oleh karena jumlah akar-akar persamaan kuadrat lebih kecil dari nol, maka

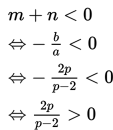
Pembuat nol pembilang : 
2p = 0 <=> p= 0

Pembuat nol penyebut : 
p – 2 = 0 <=> p = 2

Jadi, batas-batas nilai p yang memenuhi adalah {p ∈ ℝ | p < 0 atau p > 2}.

Contoh 3:

Seorang ahli gizi wajib mempertimbangkan beberapa faktor saat merancang pola makanan bernutrisi, seperti berat badan dan usia. Oleh karenanya, ahli gizi mempergunakan rumus untuk mengontrol kandungan kalori dalam makanan. Jika unit batas kesehatan tertentu per hari dirumuskan dengan

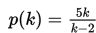
dimana k adalah jumlah kalori makanan. Tentukan batasan kalori per hari agar unit batas kesehatan tidak lebih dari 4 unit!

Penyelesaian :

Oleh karena unit batas kesehatan tidak lebih dari 4 unit, maka

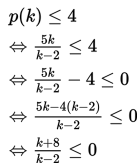
Pembuat nol pembilang :
k + 8 = 0 <=> k = -8

Pembuat nol penyebut : 
k - 2 = 0 <=> k = 2

Jadi, batasan jumlah kalori yang harus dikonsumsi per hari adalah {k ∈ ℝ | -8 ≤ k ≤ 2}.