PENERAPAN PERTIDAKSAMAAN MUTLAK PADA KEHIDUPAN SEHARI-HARI

Dalam topik kali ini, kalian akan belajar mengenai beberapa contoh pertidaksamaan nilai mutlak pada masalah nyata.

Pertidaksamaan nilai mutlak adalah pertidaksamaan yang variabelnya berada di dalam tanda mutlak. Adapaun bentuk umum pertidaksamaan nilai mutlak linear adalah sebagai berikut :

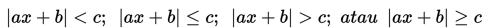
dengan a, b, c adalah konstanta dan a ≠ 0.

Selanjutnya, untuk untuk menyelesaikan pertidaksamaan nilai mutlak digunakan sifat-sifat nilai mutlak sebagai berikut :

Untuk x , a ∈ R dan a ≥ 0 berlaku :

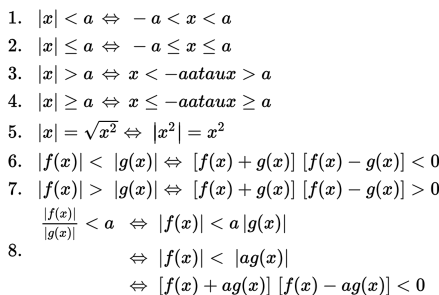
Mari kita cermati beberapa contoh soal berikut ini.

Contoh 1 :

Jarak terpendek yang diperlukan untuk menghentikan suatu mobil sejak pengereman dilakukan disebut jarak henti. Jarak henti ini merupakan faktor penting yang perlu diuji sebelum peluncuran produk mobil baru. Data mengenai jarak henti dapat digunakan untuk menghitung waktu reaksi pengemudi (selang waktu mulai pengemudi melihat kejadian sampai dia bereaksi menginjak pada rem) berdasarkan tingkat kelajuan mobil (dalam meter/jam).

Suatu penelitian menyatakan bahwa jarak henti dapat dinyatakan dengan formula :
d = |0,44v2 + 1,1v|, dimana v adalah kelajuan dan d dalam meter.

Pada batas kelajuan berapakah jarak henti mobil lebih dari 100 meter?

Penyelesaian :

Oleh karena kelajuan selalu bernilai positif, maka |0,44v2 + 1,1v| = 0,44v2 + 1,1v. Selanjutnya, agar jarak henti mobil lebih dari 100 meter, maka d haruslah lebih besar dari seratus.

Jadi, batas kelajuannya jarak henti mobil lebih dari 100 meter adalah 
-16,4 < v < 13,9 meter/jam.

Contoh 2 :

Selisih antara panjang dan lebar suatu persegi panjang kurang dari 6 cm. Jika keliling persegi panjang adalah 32 cm, maka tentukan batas nilai lebar persegi panjang tersebut!

Penyelesaian :

Oleh karena keliling persegi panjang adalah 32 cm, maka
2(p + l) = 32
<=> p + l = 16
<=> p = 16 - l

Selanjutnya, karena selisih antara panjang dan lebar persegi kurang dari 6 cm, maka

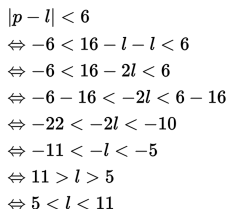
Dengan demikian, batas nilai lebar persegi panjang yang dimaksud adalah antara 5 cm sampai dengan 11 cm.

Contoh 3 :

Pergerakan suatu titik dalam koordinat kartesius ditentukan oleh nilai absis dan memenuhi pertidaksamaan |x – 1|2 + 2|x – 1| < 15. Tentukan nilai x yang memenuhi pertidaksamaan tersebut!

Penyelesaian :

Jika dimiisalkan |x – 1| = p, maka diperoleh hasil sebagai berikut :

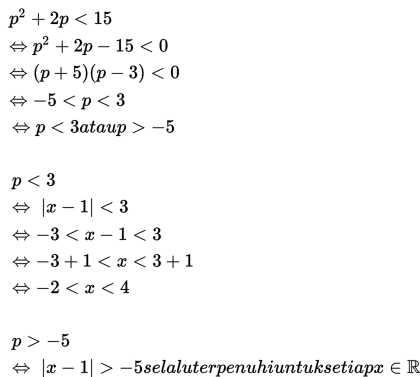
jadi, nilai x yang memenuhi adalah { x ∈ ℝ | -2 < x < 4 }.