PENGERTIAN LIMIT MELALUI PERHITUNGAN NILAI-NILAI FUNGSI

Menurut Kamus Besar Bahasa Indonesia, limit diartikan sebagai batas. Konsep limit memang berhubungan dengan batas. Akan tetapi, dalam matematika limit sering diartikan sebagai suatu nilai pendekatan. Kamu pasti bertanya-tanya bagaimana konsepnya? Agar kamu lebih mudah memahaminya, simak ilustrasi ini ya.

                             Donatur yang Teratur

Seorang donatur selalu memberikan sumbangan setiap bulan sepanjang tahun. Namun, dia menyadari bahwa jumlah uang yang dia sumbangkan setiap bulannya tidaklah memiliki keteraturan yang baik. Dia memutuskan untuk membuat suatu pola pada jumlah sumbangan per bulannya. Adapun pola yang dia pilih memenuhi fungsi:

s(t)=t2−16t−4$s(t)=\frac{t^2-16}{t-4}$

dalam jutaan rupiah, dengan variabel t menyatakan urutan bulan yang bersesuaian.

          Pada bulan februari (bulan ke-2), jumlah uang yang dia sumbangkan senilai:

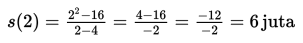
          Awalnya dia merasa puas dengan pola keteraturan yang telah dia pilih, namun pada bulan april (bulan ke-4), dia menemukan suatu keganjilan. Berdasarkan pola yang dia buat, pada bulan ke-4 dia harus menyumbangkan uang yang tidak tentu jumlahnya, yaitu:

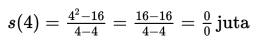
          Dia kemudian membuat sebuah tabel dari uang yang harus dia sumbangkan setiap bulannya untuk memeriksa masalah ini.

Merasa kurang yakin, donatur ini membuat tabel baru yang lebih rinci guna memeriksa jumlah sumbangan disekitar bulan ke-4.

          Dari tabel baru ini, dia berkesimpulan bahwa di sekitar bulan ke-4 dia harus menyumbangkan uang sebesar 8 juta rupiah, karena nilai fungsi pada tabel apabila ditelusuri dari kiri atau kanan cenderung menuju nilai yang sama yaitu 8.

          Nah, dari ilustrasi tersebut kita dapat belajar tentang konsep limit fungsi berdasarkan perhitungan nilai-nilai fungsi. Secara matematis, pemecahan dari masalah dalam ilustrasi dapat dinyatakan sebagai suatu limit fungsi, yaitu:

• limt→4−t2−16t−4$\underset{t\to 4^{-}}{lim}\frac{t^2-16}{t-4}$ dibaca limit fungsi t2−16t−4$\frac{t^2-16}{t-4}$ untuk t mendekati 4 dari arah kiri dan disebut sebagai limit kiri
• limt→4+t2−16t−4$\underset{t\to 4^{+}}{lim}\frac{t^2-16}{t-4}$ dibaca limit fungsi t2−16t−4$\frac{t^2-16}{t-4}$ untuk t mendekati 4 dari arah kanan dan disebut sebagai limit kanan

Oleh karena nilai limit kiri sama dengan limit kanan, maka dapat disimpulkan bahwalimt→4t2−16t−4=8$\underset{t\to 4}{lim}\frac{t^2-16}{t-4}=8$ dan dibaca limit fungsi t2−16t−4$\frac{t^2-16}{t-4}$ untuk t mendekati 4 adalah 8.

Nilai limit suatu fungsi tidak selalu ada. Adakalanya, kita menjumpai limit fungsi yang tidak mempunyai nilai di suatu titik. Untuk memahaminya, perhatikan ilustrasi di bawah ini.

                             Tarif Jasa Kurir

Tarif jasa kurir untuk pengiriman barang dalam radius 200 km pada suatu perusahaan ekspedisi dinyatakan dalam tabel berikut.

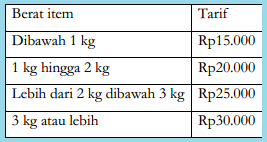
          Aturan tarif ini dapat pula dinyatakan sebagai fungsi:

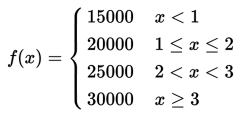
          Kita dapat menggambarkan fungsi tersebut pada sebuah grafik dengan sumbu xmerupakan berat item (kg) dan sumbu y merupakan tarif pengiriman (kali 10000) sebagai berikut.

          Untuk pengiriman barang seberat 2 kilogram dikenakan tarif 20.000 rupiah. Namun, apabila ditinjau dari sudut pandang limit fungsi, fungsi f(x) tersebut tidak memiliki nilai limit di sekitar 2 kg. Hal ini dapat dijelaskan dengan melihat tabel tarif pengiriman di sekitar nilai 2 kg.

          Perhatikan bahwa apabila kita menyusuri grafik dari kiri menuju 2 kg, hasil yang kita peroleh berbeda dengan apabila kita menyusuri grafik dari kanan menuju 2 kg. Dalam konteks limit fungsi, kondisi ini dapat dituliskan sebagai berikut.

• limx→2−f(x)=20000$\underset{x\to 2^{-}}{lim}f(x)=20000$ yang berarti limit fungsi f(x) saat x mendekati 2 dari kiri adalah 20000.
• limx→2+f(x)=25000$\underset{x\to 2^{+}}{lim}f(x)=25000$ yang berarti limit fungsi f(x) saat x mendekati 2 dari kanan adalah 25000.

Oleh karena limit kiri tidak sama dengan limit kanan atau limx→2−f(x)$\underset{x\to 2^{-}}{lim}f(x)$ ≠ limx→2+f(x)$\underset{x\to 2^{+}}{lim}f(x)$, maka nilai limit fungsi di titik tersebut tidak ada.

Dari kedua ilustrasi tersebut, dapat kita simpulkan bahwa:

TEOREMA LIMIT KIRI-LIMIT KANAN

Limit sebuah fungsi di titik x dikatakan ada jika dan hanya jika limit kiri dan limit kanannya ada dan memenuhi: limx→a−f(x)$\underset{x\to a^{-}}{lim}f(x)$ = limx→a+f(x)$\underset{x\to a^{+}}{lim}f(x)$ = limx→af(x)$\underset{x\to a}{lim}f(x)$

Dari penjelasan di atas, kita juga dapat mendefinisikan limit fungsi secara intuisi berikut.

DEFINISI LIMIT FUNGSI

limx→af(x)=L$\underset{x\to a}{lim}f(x)=L$ berarti jika x dekat tetapi berlainan dari a, maka f(x) mendekati L.

POIN PENTING

1. Limit suatu fungsi ada apabila limit kiri dan kanannya bernilai sama.
2. Limit fungsi tidak bergantung pada nilai fungsi di titik limitnya begitu pula sebaliknya.
3. Limit fungsi dapat ditentukan dengan melihat kecenderungan nilai fungsi di sekitar titik limitnya.

Kamu tentu sudah paham dengan konsep limit fungsi melalui perhitungan nilai-nilai fungsi. Agar penegetahuanmu bertambah, kamu dapat gunakan konsep tersebut untuk menghitung limit fungsi melalui pengamatan grafik fungsi seperti contoh di bawah ini.

Contoh

Perhatikan grafik dari suatu fungsi f(x) berikut.

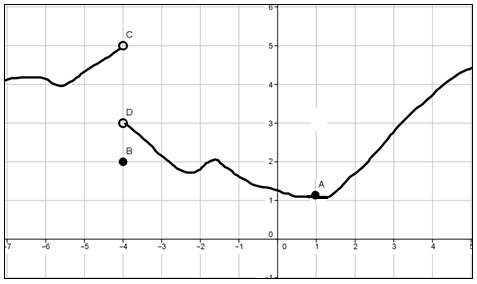
Tentukan nilai dari limit berikut.

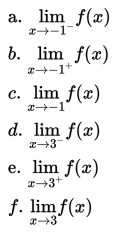
Penyelesaian:

Dengan menelusuri grafik menuju titik-titik limit yang dimaksud, diperoleh: