Penggunaan definisi geometris 1
Sudut
Sudut dapat dilihat dari karateristik mereka. Ada dua kategori yang membedakan (klasifikasi) sudut-sudut.
i). Klasifikasi didasari oleh ukuran sudut.
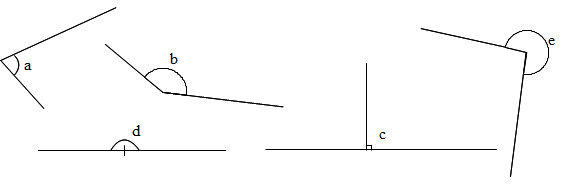
Sudut Lancip – sudut-sudut yang kurang dari 90o, contoh sudut a.
Sudut siku-siku - sudut yang tepat 90o, contoh sudut c.
Sudut Tumpul – sudut-sudut yang lebih besar 90o namun kurang dari
180o contoh sudut b.
Sudut Lurus – sudut yang besarnya sama dengan 180o, contoh sudut d.
Sudut Refleks – sudut yang besarnya kurang dari 360o namun lebih dari 180o
contoh sudut e.
Sudut
Sudut dapat dilihat dari karateristik mereka. Ada dua kategori yang membedakan (klasifikasi) sudut-sudut.
i). Klasifikasi didasari oleh ukuran sudut.
Sudut Lancip – sudut-sudut yang kurang dari 90o, contoh sudut a.
Sudut siku-siku - sudut yang tepat 90o, contoh sudut c.
Sudut Tumpul – sudut-sudut yang lebih besar 90o namun kurang dari
180o contoh sudut b.
Sudut Lurus – sudut yang besarnya sama dengan 180o, contoh sudut d.
Sudut Refleks – sudut yang besarnya kurang dari 360o namun lebih dari 180o
contoh sudut e.
ii). Sudut-sudut pada garis traversal
Diberikan dua buah garis sejajar atau lebih Given any two or more parallel lines, garis apapun yang memotong garis sejajar tersebut disebut garis traversal. Sudut-sudut mempunyai karakteristik yang akan dijelaskan tanpa pembuktian. Perhatikan diagram berikut.
Diberikan dua buah garis sejajar atau lebih Given any two or more parallel lines, garis apapun yang memotong garis sejajar tersebut disebut garis traversal. Sudut-sudut mempunyai karakteristik yang akan dijelaskan tanpa pembuktian. Perhatikan diagram berikut.
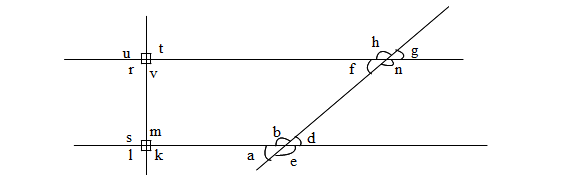
Sudut-sudut sehadap : sudut-sudut yang berada pada titik yang berbeda namun menghadap ke
arah yang sama. Sebagai contoh, sudut a dan f . Pasangan sudut sehadap lainnya adalah sudut b dan h, d dan g, e dan n. Selain itu, ada pula v dan k, m dan t, u dan s juga r dan l.
Sudut-sudut sehadap mempunyai besar sudut yang sama.
arah yang sama. Sebagai contoh, sudut a dan f . Pasangan sudut sehadap lainnya adalah sudut b dan h, d dan g, e dan n. Selain itu, ada pula v dan k, m dan t, u dan s juga r dan l.
Sudut-sudut sehadap mempunyai besar sudut yang sama.
Sudut berseberangan : sudut-sudut yang terletak pada titik yang menghadap ke
arah yang berlawanan. Besaran sudut-sudut berseberangan juga sama. Sebagai contoh, sudut d dan f adalah
sudut berseberangan. Pasangan sudut lainnya adalah sudut b dan n, r dan m, v dan s.
Sudut berseberangan vertikal. Sudut-sudut ini terletak pada titik yang sama namun menghadap
arah berlawanan. Besar sudut mereka sama. Sebagai contoh, sudut e and b,
a dan d, f dan g dan juga pasangan sudut lainnya.
Fakta lain mengenai sudut
Jumlahan Sudut-sudut yang terletak pada suatu garis lurus sama dengan 180o . Sebagai contoh n + g = 180o.
l + k = b+d = f+n = f+h = 180o.
Jumlahan sudut-sudut pada suatu titik sama dengan 360o. Contoh a+b+d+e = 360o dan u+r+v+t =
360o.
Sudut suplemen – sudut-sudut yang saling menjumlah menjadi 180o. Sudut-sudut
tersebut tidak harus berada pada garis lurus. Sudut-sudut tersebut disebut juga
suplemen satu sama lain. Sebagai contoh n + g = 180o; Kita juga dapat menunjukkan bahwa
d+n = 180o.In case, n and g are supplementary angles, the
same apply to d and n. Hence n dan d saling suplemen.
Sudut-sudut komplemen. Sudut-sudut komplemen adalah sudut-sudut yang jumlahannya sama dengan 90o; dua sudut yang jumlahannya 90o disebut komplementer.
Perhatikan gambar berikut dibawah
Fakta lain mengenai sudut
Jumlahan Sudut-sudut yang terletak pada suatu garis lurus sama dengan 180o . Sebagai contoh n + g = 180o.
l + k = b+d = f+n = f+h = 180o.
Jumlahan sudut-sudut pada suatu titik sama dengan 360o. Contoh a+b+d+e = 360o dan u+r+v+t =
360o.
Sudut suplemen – sudut-sudut yang saling menjumlah menjadi 180o. Sudut-sudut
tersebut tidak harus berada pada garis lurus. Sudut-sudut tersebut disebut juga
suplemen satu sama lain. Sebagai contoh n + g = 180o; Kita juga dapat menunjukkan bahwa
d+n = 180o.In case, n and g are supplementary angles, the
same apply to d and n. Hence n dan d saling suplemen.
Sudut-sudut komplemen. Sudut-sudut komplemen adalah sudut-sudut yang jumlahannya sama dengan 90o; dua sudut yang jumlahannya 90o disebut komplementer.
Perhatikan gambar berikut dibawah
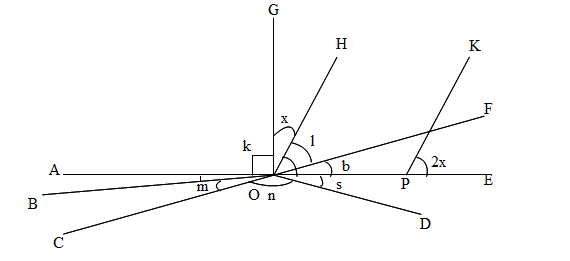
Pada gambar diatas, sudut k adalah sudut siku-siku dan AE adalah sudut lurus, sehingga
sudut k + sudut GOE = 180o, sehingga mereka adalah sudut-sudut suplementer.
karena k = 90o, sudut GOE = 90o .
sudut HOE=KPE = 2x (sudut – sudut sehadap)
namun sudut GOH+ sudut HOE = sudut GOE = 90o.
oleh karena itu x+2x = 90o or 3x = 90om
x = 30o
oleh karena itu sudut GOH = X = 30o merupakan sudut tumpul.
Kita juga bisa lihat bahwa
sudut AOB+m+n+s = 180o
sehingga sudut AOB = 180o- m - n - s
Garis AB dan CF adalah garis lurus, sehingga
sudut b = m + sudut AOB (suduts vertikal berseberangan)
Bentuk-bentuk pada Bidang
Potongan-potongangaris dengan kriteria tertentu dapat menghasilkan bentuk-bentuk yang berbeda.
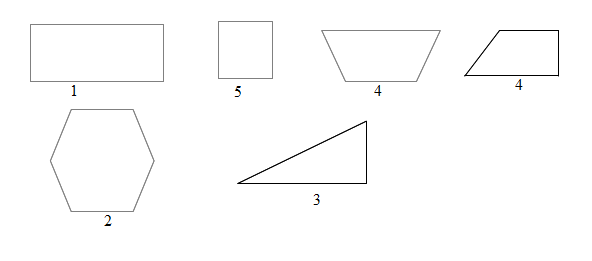
Sebagai contoh, ketika tiga potongan garis dihubungkan dari ujung ke ujung, terbentuklah sebuah segitiga. Bentuk-bentuk lain adalah persegipanjang, (1), segienam (2), Segitiga Siku-siku (3), trapesium (4), persegi (5) dan lain-lain. Bentuk-bentuk tersebut diberikan pada gambar berikut.
sudut k + sudut GOE = 180o, sehingga mereka adalah sudut-sudut suplementer.
karena k = 90o, sudut GOE = 90o .
sudut HOE=KPE = 2x (sudut – sudut sehadap)
namun sudut GOH+ sudut HOE = sudut GOE = 90o.
oleh karena itu x+2x = 90o or 3x = 90om
x = 30o
oleh karena itu sudut GOH = X = 30o merupakan sudut tumpul.
Kita juga bisa lihat bahwa
sudut AOB+m+n+s = 180o
sehingga sudut AOB = 180o- m - n - s
Garis AB dan CF adalah garis lurus, sehingga
sudut b = m + sudut AOB (suduts vertikal berseberangan)
Bentuk-bentuk pada Bidang
Potongan-potongangaris dengan kriteria tertentu dapat menghasilkan bentuk-bentuk yang berbeda.
Sebagai contoh, ketika tiga potongan garis dihubungkan dari ujung ke ujung, terbentuklah sebuah segitiga. Bentuk-bentuk lain adalah persegipanjang, (1), segienam (2), Segitiga Siku-siku (3), trapesium (4), persegi (5) dan lain-lain. Bentuk-bentuk tersebut diberikan pada gambar berikut.
Bagian dari sebuah lingkaran
Cakupan area berikut merupakan bagian dari lingkaran
Cakupan area berikut merupakan bagian dari lingkaran
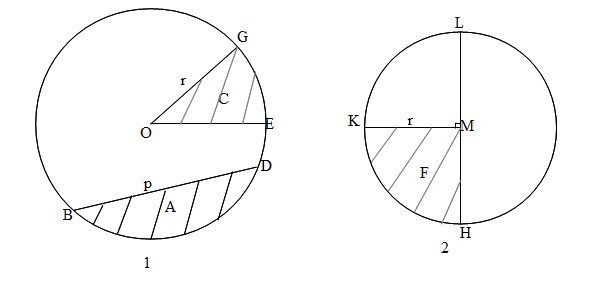
Masing-masing titik O dan M adalah titik pusat dari lingkaran 1 dan 2.
Suatu busur adalah sepotong lingkaran yang bentuknya mirip dengan kue pai. Contohnya GE, ED dan lainnya.
Garis BD disebut tali busur. Garis ini menyentuh busur lingkaran namun
tidak memotong titik pusat.
OG = OE = jari-jari lingkaran = 1. KM=HM=LM = jari-jari sementara LM adalah
diameter lingkaran 2.
Daerah C disebut juga sektor/juring. Sebuah sektor/juring adalah daerah yang dibentuk oleh dua jari-jari dan
sebuah busur lingkaran. Sektor C merupakn sektor minor sementara daerah sisanya merupakan
sektor mayor.
Daerah F adalah tipe khusus dari sektor yangdisebut kuadran. Radius yang membentuknya The radius enclosing it
harus membentuk sudut siku-siku agar dapat disebut kuadran. Daerah kuadran luasnya seperempat
dari lingkaran.
Area A disebut juga segment/tembereng. Daerah A dibentuk dari sebuah tali busur dan sebagian dari busur. Daerah A merupakan
segmen minor sementara sisa daerah dalam lingkaran merupakan segmen mayor
Daerah yang dibentuk dari diameter (HL) dan tali busur HKL disebut juga semilingkaran atau setengah lingkaran
Suatu busur adalah sepotong lingkaran yang bentuknya mirip dengan kue pai. Contohnya GE, ED dan lainnya.
Garis BD disebut tali busur. Garis ini menyentuh busur lingkaran namun
tidak memotong titik pusat.
OG = OE = jari-jari lingkaran = 1. KM=HM=LM = jari-jari sementara LM adalah
diameter lingkaran 2.
Daerah C disebut juga sektor/juring. Sebuah sektor/juring adalah daerah yang dibentuk oleh dua jari-jari dan
sebuah busur lingkaran. Sektor C merupakn sektor minor sementara daerah sisanya merupakan
sektor mayor.
Daerah F adalah tipe khusus dari sektor yangdisebut kuadran. Radius yang membentuknya The radius enclosing it
harus membentuk sudut siku-siku agar dapat disebut kuadran. Daerah kuadran luasnya seperempat
dari lingkaran.
Area A disebut juga segment/tembereng. Daerah A dibentuk dari sebuah tali busur dan sebagian dari busur. Daerah A merupakan
segmen minor sementara sisa daerah dalam lingkaran merupakan segmen mayor
Daerah yang dibentuk dari diameter (HL) dan tali busur HKL disebut juga semilingkaran atau setengah lingkaran
0 komentar:
Post a Comment