Pertidaksamaan nilai mutlak adalah pertidaksamaan yang variabelnya berada di dalam tanda mutlak. Bentuk umum pertidaksamaan nilai mutlak linear adalah:
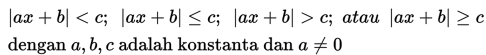
Sifat-sifat nilai mutlak berikut ini dapat kita gunakan untuk menyelesaikan pertidaksamaan nilai mutlak.
Sifat
Untuk x, a ∈ R dan a ≥ 0 berlaku :
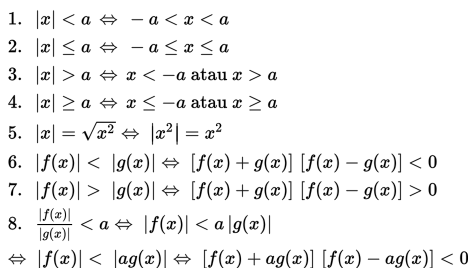
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Tentukan penyelesaian dari pertidaksamaan nilai mutlak|3x - 5| > 1
Penyelesaian :
Dengan menggunakan sifat |x| > a <=> x < -a atau x > a, maka diperoleh :
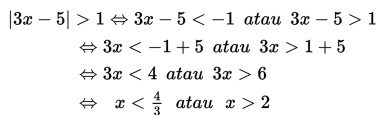
Contoh 2 :
Carilah himpunan penyelesaian dari pertidaksamaan nilai mutlak |x – 2| ≤ |x + 1|
Penyelesaian :
|x – 2| ≤ |x + 1| memenuhi bentuk |f(x)| ≤ |g(x)| dan ekuivalen dengan f2 (x) ≤ g2 (x), sehingga diperoleh :
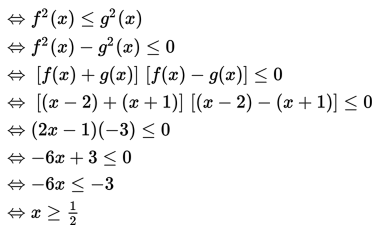
Jadi, himpunan penyelesaiannya adalah
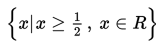
Contoh 3 :
Selesaikan pertidaksamaan :
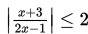
Penyelesaian :

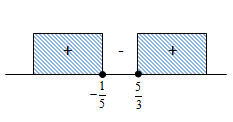
Jadi, himpunan penyelesaiannya adalah :
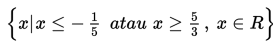
Bung penyelesaian no 3 yg dr tanda nya diganti mjd lbh besar sama dg 0, knp 5x +1 nya tidak berubah tanda juga? Jadi -5x-1
ReplyDeleteKarena udah diubah yg di -3x+5
DeleteCukup kita kalikan salah satu faktornya saja
Maksudnya supaya x-nya tidak negatif, begitu ya pak?
Delete