Pada topik yang telah lalu, kalian telah belajar mengenai persamaan pecahan.
Apakah kalian masih ingat?
Apakah kalian masih ingat?
Dalam topik ini, kalian akan belajar mengenai pertidaksamaan pecahan.
Apa yang dimaksud dengan pertidaksamaan pecahan?
Apa yang dimaksud dengan pertidaksamaan pecahan?
Pertidaksamaan pecahan adalah adalah pertidaksamaan yang melibatkan persamaan pembilang dan penyebut dengan tanda pertidaksamaan (<, ≤, >, ≥). Pertidaksamaan pecahan ada banyak bentuk dan variasinya.
Contoh :
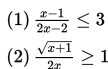
Peridaksamaan (1) adalah contoh pertidaksamaan pecahan yang melibatkan pertidaksamaan linear pada pembilang dan penyebutnya. Adapun pertidaksamaan (2) adalah pertidaksamaan pecahan yang melibatkan pertidaksamaan irrasional.
Bagaimanakah bentuk baku dari pertidaksamaan pecahan?
Ada 4 bentuk baku dari pertidaksamaan pecahan, yaitu :
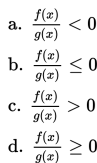
dengan syarat g(x) ≠ 0
Contoh 1
Tentukan himpunan penyelesaian dari
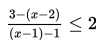
Penyelesaian :
Yang perlu dilakukan adalah menyederhanakan ruas kiri terlebih dahulu, sehingga diperoleh hasil sebagai berikut :
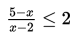
Selanjutnya, kita perlu memindahkan semua elemen pada ruas kanan ke ruas kiri, kemudian menyederhanakannya.
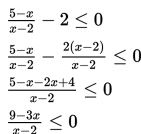
Pembuat nol dari pembilang dan penyebut pada pecahan di atas adalah x = 3 dan x = 2
Langkah selanjutnya adalah melakukan uji titik. Misal diambil x = 0 sebagai titik uji, maka diperoleh :
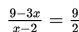
Karena untuk x = 0 diperoleh hasil positif, maka daerah pada x < 2 bernilai positif, daerah pada interval 2 < x ≤ 3 bernilai negatif, dan daerah pada x > 3 bernilai positif.
Jadi, himpunan penyelesaian pertidaksamaan di atas adalah {x ∈ ℝ | 2 < x ≤ 3}
Untuk lebih jelasnya, mari perhatikan daerah arsiran pada garis bilangan berikut ini :
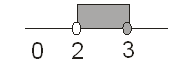
Ingat, x = 2 bukan penyelesaian karena merupakan pembuat nol dari penyebut.
Contoh 2
Tentukan himpunan penyelesaian dari
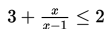
Penyelesaian :
Yang perlu dilakukan adalah memindahkan semua elemen di ruas kanan ke ruas kiri terlebih dahulu, sehingga diperoleh hasil sebagai berikut :
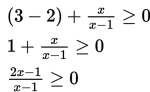
Pembuat nol dari pembilang dan penyebut dari pecahan di atas adalah x = 1/2 dan x = 1
Langkah selanjutnya adalah melakukan uji titik. Misal diambil x = 0 sebagai titik uji, maka diperoleh :
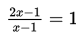
Karena untuk x = 0 diperoleh hasil positif, maka daerah pada x ≤ ½ bernilai positif, daerah pada interval ½ ≤ x < 1 bernilai negatif, dan daerah pada x > 1 bernilai positif.
Jadi, himpunan penyelesaian pertidaksamaan di atas adalah {x ∈ ℝ | x ≤ ½ atau x > 1}
Untuk lebih jelasnya, mari perhatikan daerah arsiran pada garis bilangan berikut ini :
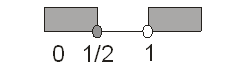
Ingat, x = 1 bukan penyelesaian karena merupakan pembuat nol penyebut.


pak ada yang salah itu yang "Misal diambil x = 0 sebagai titik uji, maka diperoleh :" itu hasilnya -9/2 bukan 9/2
ReplyDeleteWahh terima kasih sudah mengoreksi... Ia benar harusnya -9/2 .. otomatia daerah penyelesaian salah ...
DeleteThis comment has been removed by the author.
ReplyDeletePak mau tanya agar (p+1)x^2-2px+(p-4)bernilai negatif untuk semua x,maka batas-batas nilai p adalah jawab.terimakasih
ReplyDeleteAmbil diskriminan >= 0
DeleteTerus chek batas untuk tiap nilai p yang diperoleh sehingga bernilai negatif untuk semua x