Kamu telah mengetahui bahwa suatu fungsi akan menghasilkan invers yang juga merupakan fungsi bijektif. Pada pembahasan kali ini, kita akan fokus pada sifat-sifat dari fungsi invers beserta kaitannya dengan komposisi fungsi.
Misalkan fungsi f (x) dan g (x) merupakan fungsi-fungsi yang bijektif, maka invers dari kedua fungsi ini yaitu f -1 (x) dan g -1 (x) pastilah merupakan fungsi serta (f o g) (x), (g o f) (x),
(f -1 o g -1 ) (x), (g -1 o f -1 ) (x) dan komposisi lainnya juga mungkin merupakan fungsi. Pelajari diagram berikut ini dengan seksama.
(f -1 o g -1 ) (x), (g -1 o f -1 ) (x) dan komposisi lainnya juga mungkin merupakan fungsi. Pelajari diagram berikut ini dengan seksama.
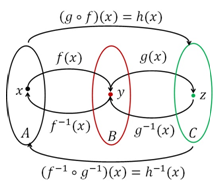
Dari diagram di atas diketahui bahwa, fungsi f (x) memetakan setiap anggota dari himpunan A ke himpunan B dan g (x ) melanjutkan pemetaan ini dari setiap anggota di himpunan B ke himpunan C, sehingga fungsi komposisi (g o f) (x) memetakan setiap anggota di himpunan A langsung ke himpunan C.
Invers dari fungsi-fungsi tersebut melakukan pemetaan yang berkebalikan yaitu g -1 (x) memetakan setiap anggota dari himpunan C ke himpunan B, dan f -1 (x) melanjutkan pemetaan dari himpunan B ke himpunan A, sehingga fungsi komposisi dari fungsi-fungsi invers ini yaitu (f -1 o g -1 ) (x) memetakan setiap anggota dari himpunan C langsung ke himpunan A. Dari penjelasan diatas dapat kita simpulkan sifat-sifat fungsi invers sebagai berikut.
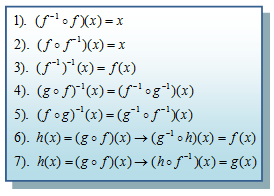
Untuk memahami lebih jauh penerapan sifat-sifat ini, mari kita pelajari beberapa contoh berikut.
Contoh 1
Diberikan dua fungsi bijektif f (x) = 3x - 2 dan g (x) = x + 6 yang keduanya memetakan anggotaɌ → Ɍ. Tentukan:
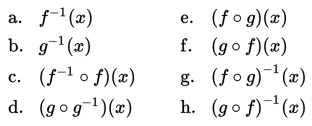
Penyelesaian:

Contoh 2
Tiga buah fungsi f, g, dan h memenuhi hubungan h (x) = g (f (x)). Apabila diketahui h (x) = 2x 2+ 8x + 12 dan g (x) = 2x + 4, maka tentukan f (x).
Penyelesaian
Dari sifat-sifat fungsi invers yang telah kita bahas sebelumnya, diketahui bahwa:
h (x) = g (f (x)) → f (x) = g -1 (h (x))
h (x) = g (f (x)) → f (x) = g -1 (h (x))
Mula-mula tentukan g -1 (x).

Selanjutnya, tentukan f (x ) dengan memanfaatkan hubungan f (x) = g -1 (h (x)).
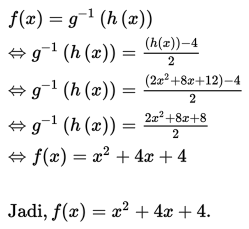
0 komentar:
Post a Comment