Soal 1
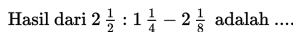
Pembahasan
Untuk menyelesaikan soal hitung campuran seperti pada soal, kita kerjakan dahulu operasi pembagiannya.
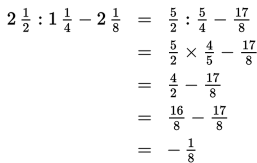
Soal 2
Perbandingan uang Ani dan Ina 3 : 5. Jumlah uang mereka Rp400.000,00. Selisih uang keduanya adalah .…
Pembahasan
Misalkan:
Jumlah uang Ani = x
Jumlah uang Ina = y
Jumlah uang Ina = y
Perbandingan uang Ani dan Ina adalah 3 : 5, berarti
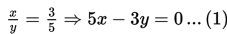
Jumlah uang Ani dan Ina adalah Rp400.000,00, berarti
x + y = 400.000 ... (2)
Kita lakukan eliminasi variabel y pada persamaan (1) dan (2), diperoleh:
5x - 3y = 0 (dikali 1) 5x - 3y = 0
x + y = 400.000 (dikali 3) 3x + 3y = 1.200.000 +
8x = 1.200.000
x = 150.000
x + y = 400.000 (dikali 3) 3x + 3y = 1.200.000 +
8x = 1.200.000
x = 150.000
Kita subsitusikan nilai x pada persamaan (2), diperoleh
x + y = 400.000
150.000 + y = 400.000
y = 250.000
150.000 + y = 400.000
y = 250.000
Jadi, selisih uang Ani dan Ina adalah Rp250.000,00 - Rp150.000,00 = Rp100.000,00.
Soal 3
Hasil dari 2-1 + 3-1 adalah ....
Pembahasan

Soal 4
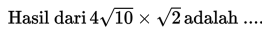
Pembahasan

Soal 5
Setelah 9 bulan uang tabungan Susi di koperasi berjumlah Rp3.815.000,00. Koperasi memberi jasa simpanan berupa bunga 12% per tahun. Tabungan awal Susi di koperasi adalah ….
Pembahasan
Susi telah menabung selama 9 bulan, berarti
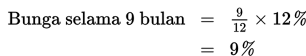
Kalian tentu masih ingat rumus menghitung tabungan awal, yaitu

Dengan demikian, tabungan awal Susi di koperasi adalah

Soal 6
Suku ke-50 dari barisan 20, 17, 14, 11, 8, … adalah
Pembahasan
Diketahui:
a = 20
b = 17 - 20 = -3
b = 17 - 20 = -3
Kalian tentu masih ingat rumus suku ke-n barisan aritmatika, yaitu
Un = a + (n - 1) b
Dengan demikian, suku ke-50 dari barisan tersebut adalah
U50 = 20 + (50 - 1) (-3)
= 20 + (-147)
= -127
= 20 + (-147)
= -127
Soal 7
Rumus suku ke-n dari barisan 2, 4, 8, 16, … adalah ….
Pembahasan
Barisan 2, 4, 8, 16, … merupakan barisan geometri dengan a = 2 dan r = 2.
Kalian tentu masih ingat rumus suku ke-n barisan geometri, yaitu
Un = a r n-1
Dengan nilai a = 2 dan r = 2, didapatkan rumus suku ke-n barisan tersebut adalah
Un = 2.2 n-1
Un = 2 n
Un = 2 n
Soal 8
Suku ke-3 dan suku ke-7 barisan aritmatika berturut-turut 10 dan 22. Jumlah 30 suku pertama barisan tersebut adalah ….
Pembahasan
Mengingat kembali rumus suku ke-n , yaitu
Un = a + (n - 1)b
Berarti,
Suku ke-7 = 22 → U7 = a + 6b = 22 ... (1)
Suku ke-3 = 10 → U3 = a + 2b = 10 ... (2)
Suku ke-3 = 10 → U3 = a + 2b = 10 ... (2)
Kita lakukan eliminasi variabel a pada persamaan (1) dan (2), diperoleh
a + 6b = 22
a + 2b = 10 _
4b = 12
b = 3
a + 2b = 10 _
4b = 12
b = 3
Dengan mensubsitusikan nilai b pada persamaan (2), kita dapatkan nilai a sebagai berikut.
a + 2b = 10
a + 2(3) =10
a = 4
a + 2(3) =10
a = 4
Kalian tentu masih ingat rumus jumlah n suku pertama deret aritmatika, yaitu
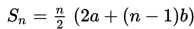
Dengan demikian, jumlah 30 suku pertama adalah
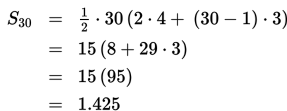
Soal 9
Perhatikan pernyataan di bawah ini.
i. 81 - y2 = (9 +y) (9 - y)
ii. x2 - x -12 = (x + 4) (x + 3)
iii. 24y2 + 6y = 6y (4y - 1)
iv. x2 + 2x - 24 = (x + 6) (x - 4)
Pernyataan yang benar adalah ....
Pembahasan
Mari kita ingat kembali bahwa:
(x + a) (x + b) = x2 + (a + b) x + ab
(x + a) (x - a) = x2 - a2
Pernyataan-pernyataan pada soal yang memenuhi sifat tersebut adalah
81 - y2 = (9 +y) (9 - y)
x2 + 2x - 24 = (x + 6) (x - 4)
Dengan demikian pernyataan yang benar adalah pernyataan i dan iv.
Soal 10
Himpunan penyelesaian dari 2x + 5 ≤ 3x - 3 untuk xbilangan bulat adalah ....
Pembahasan

Dengan demikian diperoleh himpunan penyelesaian
{x|x ≥ 8, x bilangan bulat}.
{x|x ≥ 8, x bilangan bulat}.
0 komentar:
Post a Comment