Soal 11
Tiga bilangan genap berurutan jumlahnya 84. Jumlah bilangan terbesar dan terkecil adalah .…
Pembahasan
Perhatikan 3 bilangan genap berurutan berikut : 2, 4, 6.
Jika kita perhatikan, selisih antara kedua bilangan genap yang berurutan adalah 2.
Dengan demikian, jika bilangan pertama kita misalkan dengan a, maka urutan ketiga bilangan tersebut adalah
a, a + 2 dan a + 4.
Diketahui:
Jumlah tiga bilangan genap berurutan adalah 84, berarti
a + a + 2 + a + 4 = 84
3a + 6 = 84
3a = 78
a = 26
Subsitusikan nilai a = 26 pada bilangan kedua dan ketiga, diperoleh
bilangan pertama = 26
bilangan kedua = 26 + 2 = 28
bilangan ketiga = 26 + 4 = 30
Dengan demikian, jumlah bilangan terkecil dan terbesar adalah 26 + 30 = 56.
Soal 12
Diketahui A = {x|x < 7, x bilangan asli} dan
B = {x|x ≤ 12, x bilangan prima}. A ∪ B adalah ....
Pembahasan
A = {x|x < 7, x bilangan asli} = {1, 2, 3, 4, 5, 6}
B = {x|x ≤ 12, x bilangan prima} = {2, 3, 5, 7, 11}
Dengan demikian, A ∪ B = {1, 2, 3, 4, 5, 6, 7, 11}.
Soal 13
Fungsi h didefinisikan dengan rumus h (x) = ax + b.
Jika h (5) = -8 dan h (-2) = 13, nilai h (3) adalah ….
Pembahasan
Diketahui:
h (x) = ax + b
Dengan demikian,
h (5) = -8 → 5a + b = -8 ... (1)
h (-2) = 13 → -2a + b = 13 ... (2)
Kita lakukan eliminasi variabel b pada persamaan (1) dan (2), diperoleh:
5a + b = -8
-2a + b = 13 _
7a = -21
a = -3
Selanjutnya subsitusikan nilai a pada persamaan (1)
5a + b = -8
5(-3) + b = -8
b = 7
Nilai a = -3 dan nilai b = 7, akibatnya
h (x) = ax + b = -3x + 7
h (3) = -3(3) + 7 = -9 + 7 = -2
Jadi, nilai h (3) = -2.
Soal 14
Persamaan garis yang melalui titik (2, 3) dan (-1, 4)adalah ….
Pembahasan
Kalian tentu masih ingat cara menentukan persamaan garis yang melalui titik (x1, y1) dan (x2, y2), yaitu
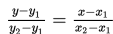
Dengan demikian, persamaan garis yang melalui titik (2, 3) dan
(-1, 4) adalah
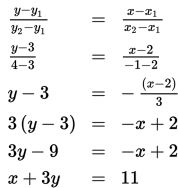
Soal 15
Gradien garis 6y + 3x = -10 adalah ….
Pembahasan
Kalian tentu masih ingat bahwa gradien garis y = mx + c adalah m.
Oleh karena itu, kita ubah bentuk persamaan pada soal menjadi bentuk
y = mx + c sehingga diperoleh
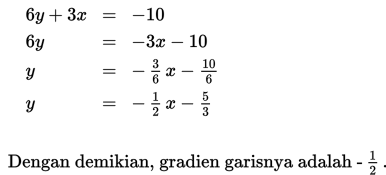
Soal 16
Ady membeli 5 pulpen dan 4 pensil dengan hargaRp30.000,00, sedangkan Wina membeli 2 pulpen dan 6pensil dengan harga Rp23.000,00. Jika Tika membeli 3pulpen dan 2 pensil, jumlah uang yang harus dibayar adalah ….
Pembahasan
Misal:
x = harga sebuah pulpen
y = harga sebuah pensil
Sistem persamaan linear dua variabel yang terbentuk adalah
5x + 4y = 30.000 ... (1)
2x + 6y = 23.000 ... (2)
Kita lakukan eliminasi variabel y pada persamaan (1) dan (2), diperoleh
5x + 4y = 30.000 (dikali 3) 15x + 12y = 90.000
2x + 6y = 23.000 (dikali 2) 4x + 12y = 46.000 _
11x = 44.000
x = 4.000
Kita subsitusikan nilai x ke persamaan (1) sehingga diperoleh
5x + 4y = 30.000
5 (4.000) + 4y = 30.000
20.000 + 4y = 30.000
4y = 10.000
y = 2.500
Dengan demikian, harga sebuah pulpen adalah Rp4.000,00 dan harga sebuah pensil adalah Rp2.500,00.
Jadi, jika Tika membeli 3 pulpen dan 2 pensil jumlah uang yang harus dibayarkan adalah
3x + 2y =3 (4.000) + 2 (2.500) = 17.000.
Soal 17
Diketahui belahketupat ABCD, panjang diagonal AC = 96 cm, dan kelilingnya 208 cm. Luas belahketupatABCD adalah .…
Pembahasan
Perhatikan gambar berikut ini.
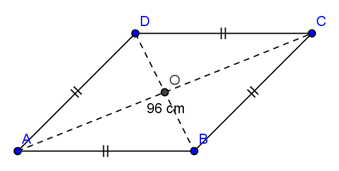
Diketahui keliling belahketupat = 208 cm
Keliling belahketupat = AB + BC + CD + DA
dengan AB = BC = CD = DA = x, maka
Keliling belahketupat = 4x
208 = 4x
x = 52
Dengan demikian, AB = BC = CD = AD = 52 cm.
Diketahui AC = 96 maka AO = 96 : 2 = 48 cm
Untuk menentukan panjang diagonal BD, terlebih dahulu akan ditentukan panjang OB.

Jadi, diagonal BD = 2 x OB = 2 x 20 = 40 cm.
Selanjutnya, kita tentukan luas belahketupat dengan cara berikut.
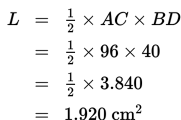
Soal 18
Perhatikan gambar berikut.
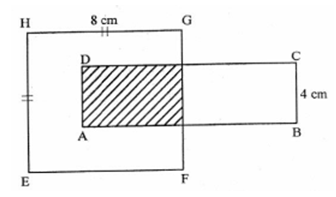
Bidang ABCD adalah persegi panjang dan bidangEFGH adalah persegi. Jika panjang AB = 12 cm dan luas daerah yang diarsir 32 cm2, luas daerah yang tidak diarsir adalah ….
Pembahasan
Berdasarkan gambar pada soal, dapat diketahui:
Luas daerah yang tidak diarsir = Luas persegipanjang + Luas persegi - 2 x Luas daerah yang diarsir
Luas daerah yang tidak diarsir = (p x l) + (s x s) - 2 (32)
Luas daerah yang tidak diarsir = (12 x 4) + (8 x 8) - 2 (32)
Luas daerah yang tidak diarsir = (48) + (64) - 2 (32)
Luas daerah yang tidak diarsir = 48 cm2
Jadi, luas daerah yang tidak diarsir adalah 48 cm2 .
Soal 19
Suatu taman berbentuk persegipanjang dengan ukuran panjang 48 m dan lebar 32 m, di sekeliling taman akan ditanami pohon cemara dengan jarak antarpohon 4 m. Banyak pohon cemara yang harus ditanam adalah ….
Pembahasan
Banyaknya pohon yang harus ditanam = keliling taman : jarak antar pohon
Keliling taman = 2 x (p + l)
= 2 x (48 + 32)
= 2 x 80
= 160 m
Banyaknya pohon = keliling taman : jarak antar pohon
= 160 : 4
= 40 pohon
Jadi, banyaknya pohon cemara yang harus ditanam adalah 40 pohon.
Soal 20
Diketahui ∆PQR kongruen dengan ∆KLM, ∠P = ∠L dan
∠R = ∠K. Pasangan sisi yang sama panjang adalah ….
Pembahasan
Berdasarkan informasi pada soal, diperoleh gambar segitiga PQR dan KLM sebagai berikut:
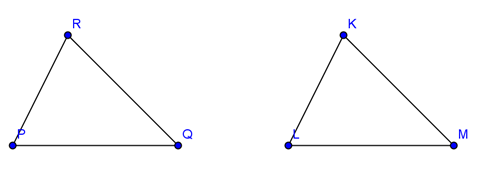
Dengan demikian pasangan sisi yang sama panjang adalah PQ = LM, QR = KM, dan PR = KL.
0 komentar:
Post a Comment