TEOREMA FAKTOR

Pembagian suku banyak P (x) dengan q (x) yang memberikan sisa S = 0 dapat kita tuliskan sebagai

                        P (x) = q (x) H (x) + 0

dengan H (x) merupakan sisa pembagian dan q (x) = (x - k) sebagai faktor linearnya. Persamaan tersebut dapat kita tuliskan ulang sebagai berikut.

                        P (x) = (x - k) H (x)

Untuk menentukan apakah (x - k) merupakan faktor linear dari P (x), maka digunakan teorema faktor berikut ini.

Teorema Faktor

Misalkan P (x) = (x - k) H (x) + S maka (x - k) merupakan faktor dari suku banyak P (x) jika dan hanya jika P (k) = 0.

Contoh 1:

Tunjukan bahwa q (x) = x - 1 merupakan faktor dari suku banyak P (x) = x3 + x2 + 2x - 4.

Penyelesaian:

Cara 1:

q (x) = x - 1 merupakan faktor dari suku banyak P (x) = x3 + x2 + 2x - 4 jika dan hanya jika pembagian 
P (x) oleh q (x) memberikan sisa 0. Mari kita gunakan metode Horner untuk mencari sisa pembagiannya.

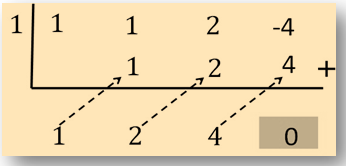
Oleh karena sisa pembagiannya 0, maka q (x) = x - 1 merupakan faktor dari suku banyak 
P (x) = x3 + x2 + 2x - 4.

Cara 2:

Dengan menggunakan Teorema Sisa I, kita tahu bahwa S = P (k) apabila suku banyak P (x)dibagi oleh (x - k). Oleh karena itu, kita hanya perlu memeriksa nilai dari P (1) sebagai berikut.

P (1) = 13 + 12 + 2(1) - 4
P (1) = 1 + 1 + 2 - 4
P (1) = 0

Jadi, q (x) = x - 1 merupakan faktor dari suku banyak P (x) = x3 + x2 + 2x - 4 karena pembagiannya memberikan sisa nol (0).

Cara 3:

Untuk melihat sisa pembagiannya, kita juga dapat menggunakan metode pembagian bersusun sebagai berikut.

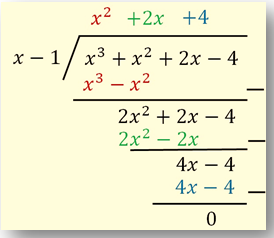
Jadi, q (x) = x - 1 merupakan faktor dari suku banyak P (x) = x3 + x2 + 2x - 4 karena pembagiannya memberikan sisa nol (0).

Menentukan Faktor-Faktor Suku Banyak

Misalkan suku banyak P (x) dapat difaktorkan kedalam bentuk berikut ini,

P (x) = q1 (x) q2 (x) q3 (x) ... qn (x)

maka P (x) akan bernilai nol saat salah satu dari q (x) bernilai nol.

Misalkan suku banyak P (x) = x4 - 5x2 + 4 dapat difaktorkan menjadi P (x) = (x - 1) (x + 1) (x - 2) (x + 2) sehingga P (x) akan bernilai nol saat x = {-2, -1, 1, 2}.

Nah, apa masalahnya sekarang? Betul, bagaimana cara mendapatkan faktor-faktor dari suku banyak tersebut? Untuk itu, mari kita pelajari contoh berikut.

Contoh 2:

Tentukan faktor-faktor dari P (x) = 6x2 - 5x + 1.

Penyelesaian:

Misalkan q (x) = (x - k) merupakan salah satu faktor dari P (x). Nilai yang mungkin untuk kadalah faktor dari suku konstan yaitu 1, faktor dari koefisien pada variabel berderajat tertinggi yaitu 6 atau rasio dari keduanya. Nilai-nilai yang mungkin untuk k kita rangkum dalam tabel berikut.

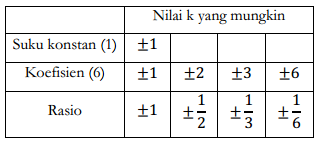
Setelah dilakukan beberapa percobaan dengan tabel Horner, didapati bahwa k=12$k=\frac{1}{2}$merupakan salah satu nilai yang memenuhi. Berikut tabel Horner yang bersesuaian untuk k=12$k=\frac{1}{2}$.

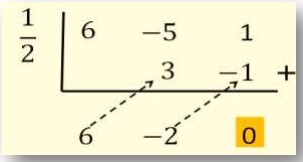
Jadi, P (x) = (x−12)(6x−2)$(x-\frac{1}{2})(6x-2)$.

Apabila kalian memfaktorkan secara langsung bentuk kuadrat suku banyak tersebut, maka kalian akan memperoleh faktor-faktor berupa P (x) = (2x - 1) (3x -1). Perhatikan bahwa meskipun kedua bentuk faktor yang kita peroleh berbeda, namun apabila kita jabarkan faktor tersebut maka akan kalian dapati bahwa keduanya setara.

Contoh 3:

Tentukan faktor-faktor dari P (x) = 2x3 - 3x2 - 3x + 2.

Penyelesaian:

Misalkan q (x) = (x - k) merupakan salah satu faktor dari P (x), maka nilai yang mungkin untukk kita rangkum dalam tabel berikut.

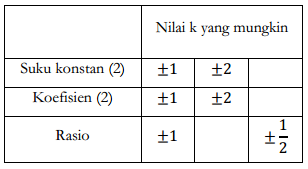
Setelah dilakukan beberapa percobaan dengan tabel Horner, didapati bahwa k = -1 merupakan nilai yang memenuhi. Adapun tabel Horner yang dimaksud adalah sebagai berikut.

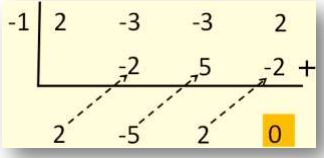
P (x) dapat ditulis sebagai P (x) = (x + 1) (2x2 - 5x + 2).

Untuk mencari faktor yang lain, kita dapat menggunakan prosedur yang sama. Setelah dilakukan beberapa percobaan dengan tabel Horner, didapati bahwa nilai k = 2 juga merupakan nilai yang memenuhi.

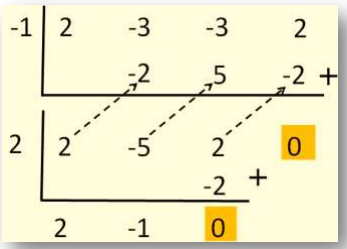
Jadi, faktor-faktor linear dari P (x) adalah P (x) = (x + 1) (x - 2) (2x - 1).