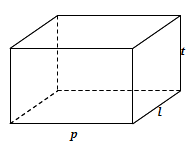
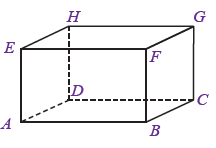
Soal Diberikan kubus ABCD.EFGH dengan panjang rusuk 5. Titik I dan J sebarang pada BF dengan IJ = 1. Titik K dan L sebarang pada CG dengan...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMP TAHUN 2016 NO 7 ISIAN
Soal Diantara 30 siswa, 15 siswa senang atletik, 17 siswa senang basket dan 17 siswa senang catur. Siswa yang senang atletik dan basket sa...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMA TAHUN 2016 NO 6 ISIAN
Soal Untuk setiap bilangan asli n, misalkan S(n) menyatakan hasil jumlah digit-digit n dalam penulisan desimal. Sebagai contoh, S(2016) = ...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMA TAHUN 2016 NO 5 ISIAN
`Soal Jika 0 < x < Ï€/2 dan 4 tan x + 9 cot x ≤ 12, maka nilai sin x yang mungkin adalah .... Pembahasan 4 tan x + 9/tan x ≤ 1...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMP TAHUN 2016`NO 4 ISIAN
Soal Titik P adalah suatu titik pada segiempat konveks ABCD dengan PA = 2, PB = 3, PC = 5, dan PD = 6. Luas maksimum segiempat ABCD adalah...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMA TAHUN 2016 NO 3 ISIAN
Soal Tiga bilangan berbeda a, b, c akan dipilih satu persatu secara acak dari 1, 2, 3, 4, ..., 10 dengan memperhatikan urutan. Probabilita...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMA TAHUN 2016 NO 2 ISIAN
Soal Suatu fungsi f mempunyai sifat f(65x + 1) = x² – x + 1 untuk semua bilangan real x. Nilai f(2016) adalah .... Pembahasan 65x + 1 =...
Read More
SOAL DAN PEMBAHASAN OSP MATEMATIKA SMA TAHUN 2016 NO 1 ISIAN
Soal Misalkan a, b, c tiga bilangan asli yang memenuhi 2^a + 2^b + 2^c = 100. Nilai dari a + b + c adalah .... Pembahasan 2^2+2^5+2^6 ...
Read More
LUAS PERMUKAAN PRISMA
Perhatikan gambar prisma berikut ini. Gambar di atas merupakan salah satu contoh prisma yang disebut prisma segitiga. Dinamakan demiki...
Read More
LUAS PERMUKAAN BALOK
Perhatikan gambar balok berikut ini. Permukaan sebuah balok terdiri atas 6 buah persegi panjang, sehingga luas permukaan sebuah balok s...
Read More
JARING-JARING LIMAS
Limas adalah bangun ruang yang memiliki satu bidang alas dan bidang-bidang tegak berbentuk segitiga yang bertemu pada satu titik puncak. Sa...
Read More
JARING-JARING PRISMA
risma adalah bangun ruang yang memiliki sepasang bidang sejajar dengan ukuran dan bentuk yang sama sebagai alas dan tutupnya, sedangkan bid...
Read More
JARING-JARING BALOK
Perhatikan gambar balok di bawah ini. Jika balok ABCD.EFGH ini dipotong pada rusuk tertentu, maka akan membentuk bangun datar, sepert...
Read More
JARING-JARING KUBUS
Perhatikan gambar kubus di bawah ini. Jika kubus ABCD.EFGH ini kita potong, maka akan membentuk bangun datar, seperti pada gambar ber...
Read More
VOLUME KUBUS
Perhatikan gambar kubus berikut ini. Volum sebuah kubus dengan rusuk s dapat ditentukan dengan rumus berikut ini : Contoh Seb...
Read More
LUAS PERMUKAAN KUBUS
Perhatikan gambar kubus berikut ini. Permukaan sebuah kubus terdiri atas 6 buah persegi yang kongruen, sehingga luas permukaan sebuah k...
Read More
SOLUSI OSK MATEMATIKA SMP 2016 (DOWNLOAD)
Silahkan download solusi osk matematika smp 2016 berikut SOLUSI OSK MATEMATIKA SMP 2016 Sumber : Saifur Arif
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 15 PILGANDA
Soal Terdapat lima bilangan bulat positif dengan rata rata 40 dan jangkauan 10. Nilai maksimum yang mungkin untuk bilangan terbesar dari l...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 14 PILGANDA
Soal Diatas meja terdapat dua set kartu. Setiap kartu terdiri atas 52 lembar dengan empat warna berbeda (merah, kuning, hijau, dan biru). ...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 13 PILGANDA
Soal Pembahasan Jadi rata rata produk B adalah (800 + 600 + 3600 + 400) /4 = 200 + 150 + 900 + 100 = 1350
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 12 PILGANDA
Soal Banyak bilangan bulat k > -20 sehingga parabola y = x^2 + k tidak berpotongan dengan lingkaran x^2 + y^2 = 9 adalah Pembahasan ...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 11 PILGANDA
Soal Suatu fungsi ditentukan dengan rumus f(x) = 2x + 1 untuk x genap dan f(x) = 2x – 1 untuk x ganjil. Jika a adalah bilangan asli, maka...
Read More
SOAL OSK MATEMATIKA SMP 2016 (DOWNLOAD)
Silahkan download soal osk matematika smp 2016 berikut ini SOAL OSK MATEMATIKA SMP 2016 Sumber : saifur arif
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 10 PILGANDA
Soal Suatu survei dilakukan pada siswa kelas VII untuk mengetahui siswa yang berminat mengikuti kegiatan Paskibra. Hasil survei adalah se...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 9 PILGANDA
Soa l Jika sistem persamaan mx + 3y = 21 4x - 3y = 0 Memiliki penyelesaian bilangan bulat x dan y. Maka nilai m + x + y yang mungkin...
Read More
SOAL: DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 8 PILGANDA
Soal Banyak bilangan real x yang memenuhi x²°¹⁶ – x²°¹⁴ = x²°¹⁵ – x²°¹³ adalah .... Pembahasan x^2016 - x^2014 - x^2015 + x^2013 = 0 ...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 7 PILGANDA
Soal Pada pagi hari yang cerah, suatu bola raksasa ditempatkan ditanah lapang yang datar. Panjang bayangan bola tersebut apabila diukur da...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 6 PILGANDA
SOAL Perhatikan gambar dibawah ini. Jika BE = 2 cm, EF = 6 cm, dan FC = 4 cm, maka panjang DE adalah .... cm Pembahsan AF = √(BF ...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 5 PILGANDA
Soal Diketahui dua titik A(1, 1) dan B(12, -1). Garis â„“ dengan gradien -3/4 melalui titik B. Jarak antara titik A dan garis â„“ adalah .... ...
Read More
SOAL DAN PEMBAHASAN OSK MATEMATIKA SMP 2016 NO 4 PILGANDA
Soal Diketahui ABCD dan CEGH adalah dua persegi panjang kongruen dengan panjang 17 cm dan lebar 8 cm. Titik F adalah titik potong sisi AD ...
Read More
Subscribe to:
Posts
(
Atom
)