SIFAT-SIFAT SEGITIGA YANG SEBANGUN

Perhatikan gambar berikut.

       Diketahui ΔABC sebangun dengan ΔKLM. Untuk membuktikan kesebangunan kedua segitiga tersebut, bandingkan sisi-sisi dan sudut-sudut yang bersesuaian. Untuk membandingkan sisi–sisi yang bersesuaian (seletak), perhatikan sisi di depan sudut yang berukuran sama. Dari gambar di atas, perbandingan sisi yang bersesuaian pada segitiga ABC dan KLM yaitu:

BCLM=CAMK=ABKL

⇔a2a=b2b=c2c=12

Selain itu, dari sudut-sudut yang bersesuaian diperoleh:

∠ACB = ∠ KML
∠CAB = ∠MKL
Ini berarti, ∠ABC = ∠KLM

Berdasarkan uraian di atas, diperoleh kesimpulan sebagai berikut.

Sifat–Sifat Segitiga yang Sebangun

• Sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai.
• Sudut–sudut yang bersesuaian sama besar.

Untuk memeriksa kesebangunan pada segitiga, lakukan pengujian terhadap unsur-unsur yang diketahui berdasarkan syarat-syarat kesebangunan segitiga pada tabel di bawah ini.

Contoh 1

Perhatikan gambar berikut.

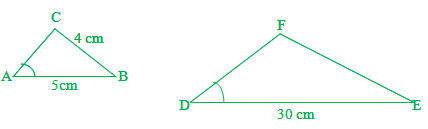
Jika segitiga ABC sebangun dengan DEF, maka tentukan panjang sisi EF.

Penyelesaian:

Diketahui:
panjang sisi AB = 5 cm
panjang sisi BC = 4 cm
panjang sisi DE = 30 cm

ABDE=BCEF

⇔530=4EF

⇔16=4EF

⇔EF=24

Jadi, panjang sisi EF adalah 24 cm.

Contoh 2

Perhatikan gambar berikut.

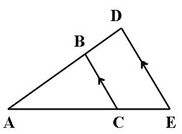
Tentukan syarat-syarat yang dipenuhi agar ΔABC sebangun dengan ΔADE.

Penyelesaian:

ΔABC sebangun dengan ΔADE karena:

• ∠BAC berimpit dengan ∠DAE sehingga besarnya sama.
• besar ∠ABC = ∠ADE karena keduanya adalah sudut-sudut sehadap.
• besar ∠ACB = ∠AED karena keduanya adalah sudut-sudut sehadap.

Jadi, ΔABC sebangun dengan ΔADE karena memenuhi syarat sudut, sudut, sudut (sd, sd, sd).

Contoh 3

Perhatikan gambar berikut.

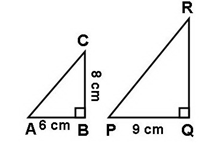
Jika ΔABC sebangun dengan ΔPQR, maka tentukan:

• syarat yang dipenuhi agar segitiga tersebut sebangun.
• panjang sisi QR.
• panjang sisi PR

Penyelesaian:

Diketahui:
ΔABC sebangun dengan ΔPQR
panjang sisi AB = 6 cm
panjang sisi BC = 8 cm
∠ABC = 90⁰ (sudut siku-siku)
panjang sisi PQ = 9 cm
∠PQR = 90⁰ (sudut siku-siku)

• Syarat yang dipenuhi agar ΔABC sebangun dengan ΔPQR

Ini berarti:
sisi AB bersesuaian dengan PQ
sisi BC bersesuaian dengan QR
∠ABC bersesuaian dengan ∠PQR

Jadi, syarat yang memenuhi segitiga tersebut sebangun adalah sisi, sudut, sisi (s, sd, s).

• Panjang sisi QR

Tentukan perbandingan sisi-sisi yang bersesuaian pada ΔABC dan ΔPQR.

ABPQ=BCQR=ACPR

Panjang sisi QR adalah:

ABPQ=BCQR

⇔69=8QR

⇔23=8QR

⇔2QR=24

⇔QR=12

Jadi, panjang QR = 12 cm.

• Panjang sisi PR

Panjang sisi PR dapat ditentukan dengan menggunakan teorema Pythagoras.

PR2 = PQ2 + QR2
⇔ PR2 = 92 + 122
⇔ PR2 = 81 + 144
⇔ PR2 = 225
⇔ PR = 15

Jadi, panjang sisi PR adalah 15 cm.