Berikut soal dari pembaca yang penulis terima via bbm Pembahasan Bentuk diatas sudah berhasil kita buktikan.. selanjutnya S...
Read More
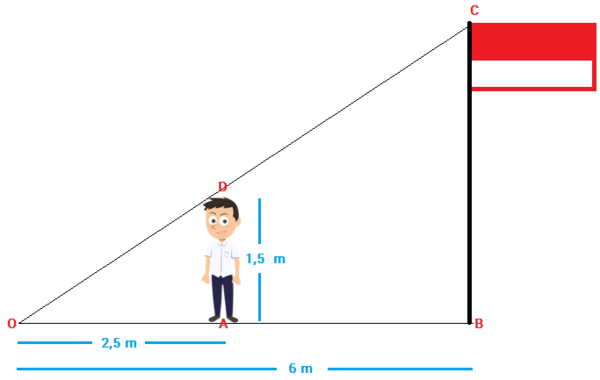
Menyelesaikan Masalah Matematika Terkait Kekongruenan dan Kesebangunan
Dalam kehidupan sehari-hari sering kita jumpai benda-benda dengan bentuk dan ukuran yang sama. Sebagai contoh keramik-keramik yang terpasan...
Read More
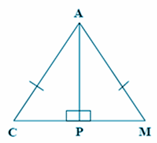
KEKONGRUENAN PADA SEGITIGA
Kongruen dilambangkan dengan ≅ , sehingga jika terdapat dua buah segitiga yang kongruen misalnya ΔABC kongruen dengan ΔPQR, maka dapat ...
Read More
Subscribe to:
Posts
(
Atom
)