VOLUME TABUNG

 Pada topik sebelumnya, kalian telah belajar tentang unsur tabung. Tabung dibentuk dari dua buah lingkaran yang menjadi alas dan tutupnya, serta selimut yang menjadi sisi tegaknya. Dua buah lingkaran yang saling berhadapan tersebut memiliki bentuk dan ukuran yang sama (kongruen).

        Coba perhatikan gambar di bawah ini.

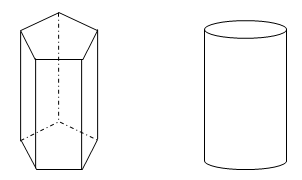
        Masih ingatkah kalian cara mencari volume prisma? Ya, benar sekali. Untuk mencari volume prisma, kita bisa gunakan rumus:

volume prisma = luas alas × tinggi

Kalau kita amati dengan baik, bentuk prisma dan tabung memiliki susunan yang mirip. Tabung merupakan sebuah prisma yang alasnya berupa lingkaran. Masih ingatkah kalian tentang luas lingkaran? Ya, benar sekali. Luas Lingkaran = πr2 .

Dengan demikian, kita dapat tentukan rumus volume tabung sebagai berikut.

Volume tabung = luas alas × tinggi

Volume tabung = πr2t

dengan:

r = panjang jari-jari tabung;

t = tinggi tabung; dan

π=227$\pi =\frac{22}{7}$ atau π = 3,14.

Contoh 1:

Sebuah tabung memiliki jari-jari 10 cm dan tinggi 20 cm. Tentukan:

a. Luas alasnya

b. Volume

Penyelesaian:

Dari soal, diketahui:

r = 10 cm

t = 20 cm

Dengan demikian, kita peroleh:

a. Luas alas tabung berupa lingkaran. Dengan demikian, untuk mencari luas alasnya, kita gunakan rumus luas lingkaran.

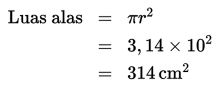
b. Volume tabung dapat ditentukan dengan cara berikut.

Contoh 2:

Sebuah tabung memiliki jari-jari 21 cm dan tinggi 10 cm. Tentukan volume tabung tersebut.

Penyelesaian:

Dari soal, diketahui:

r = 21 cm

t = 10 cm

Dengan demikian, diperoleh:

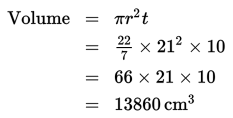
Jadi, volume tabungnya adalah 13860 cm³.