Jika , , , ... adalah suku-suku barisan aritmetika, maka + + + ... disebut dengan deret aritmetika. Jadi, suku-suku dari suatu deret aritmetika berasal dari barisan aritmetika. Dengan kata lain, deret aritmetika merupakan jumlah suku-suku suatu barisan aritmetika.
Bagaimana cara menentukan jumlah n suku pertama suatu deret aritmetika? Kamu dapat menentukan jumlah n suku pertama deret aritmetika dengan menggunakan rumus:
= n (a + ) atau = n (2a + (n - 1) b)
Untuk suku ke-n suatu deret aritmetika dapat ditentukan dengan rumus,
= -
= -
Kamu juga dapat menggunakan rumus suku ke-n pada barisan aritmetika yaitu,
= a + (n - 1) b
= a + (n - 1) b
Contoh 1
Hitunglah jumlah dari deret artimetika 3 + 5 + 7 + ... + 15.
Penyelesaian:
Diketahui deret aritmetika 3 + 5 + 7 + ... + 15.
Diketahui deret aritmetika 3 + 5 + 7 + ... + 15.
Dari deret tersebut diperoleh informasi bahwa, a = 3, b = 2 dan = 15.
Mula-mula tentukan nilai n-nya, agar kita dapat menggunakan rumus = n (a + ).
Cara untuk menentukan nilai n adalah sebagai berikut.
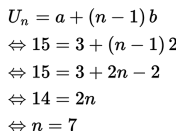
Ternyata, 15 adalah suku ke 7 () atau nilai n = 7,
Selanjutnya, tentukan hasil penjumlahan ketujuh suku () dari 1 + 3 + 7 + ... + 15 dengan mengganti a = 3, = 15 dan n = 7 ke
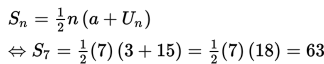
Jadi, jumlah dari 3 + 5 + 7 + ... + 15 adalah 63.
Contoh 2
Jumlah n suku pertama suatu deret aritmetika ditentukan oleh rumus . Tentukan suku ke-5 deret tersebut.
Penyelesaian:
Ingat bahwa suku ke-n suatu deret aritmetika ditentukan melalui rumus = - .
Ingat bahwa suku ke-n suatu deret aritmetika ditentukan melalui rumus = - .
Mula-mula tentukan dengan mengganti setiap n dengan (n - 1) pada .
Oleh karena , maka
Oleh karena penjabaran dari , maka
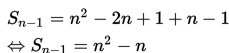
Selanjutnya, tentukan rumus suku ke-n () dengan mengganti dan ke rumus = - sebagai berikut.
= =
Ganti n = 5 ke sehingga,
= (2) (5) = 10
0 komentar:
Post a Comment