Apa hubungan antara barisan geometri dan deret geometri? Jika adalah suku-suku barisan geometri, maka disebut deret geometri. Jadi, suku-suku dari suatu deret geometri berasal dari barisan geometri. Misalnya, pada contoh di atas telah diketahui bahwa 1, 2, 4, 8, 16, … merupakan barisan geometri, maka 1 + 2 + 4 + 8 + 16 + … merupakan deret geometri. Dengan demikian diperoleh bentuk umum untuk deret geometri, yaitu:
Dengan,
a = suku pertama
r= rasio atau perbandingan
a = suku pertama
r= rasio atau perbandingan
Seperti deret aritmetika, untuk menentukan jumlah n suku suatu deret geometri akan sangat tidak efektif apabila kita menjumlahkan suku-sukunya satu persatu. Hal ini karena membutuhkan waktu yang lebih lama dan sering terjadi kesalahan. Untuk itu, dibutuhkan cara khusus untuk menghitung jumlah n suku pertama () suatu deret geometri. Ada dua rumus yang digunakan untuk menghitung suatu deret geometri. Penggunaan rumus tersebut tergantung jenis deret geometrinya. Berikut diuraikan jenis-jenis deret geometri beserta rumus yang digunakan.
Deret Naik
Rumus jumlah n suku pertamanya adalah,
, untuk r > 1 dan r ≠ 1
, untuk r > 1 dan r ≠ 1
Contoh Deret Naik
Deret geometri 1 + 2 + 4 + 8 + 16 + ...
Deret tersebut disebut deret naik karena nilai suku-sukunya semakin meningkat dengan r > 1. Perhatikan ilustrasi berikut.
Deret geometri 1 + 2 + 4 + 8 + 16 + ...
Deret tersebut disebut deret naik karena nilai suku-sukunya semakin meningkat dengan r > 1. Perhatikan ilustrasi berikut.
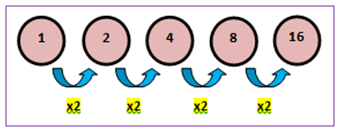
Dari ilustrasi diperoleh bahwa, = 1 dan = 2.
Sehingga, dapat dicari nilai r
Sehingga, dapat dicari nilai r
Catatan: Kamu boleh memilih cara yang kamu anggap paling mudah untuk menentukan r, baik dengan cara ilustrasi maupun dengan rumus
Oleh karena nilai r = 2 yang artinya r > 1 maka gunakan rumus untuk deret naik.
Misalkan kita akan menghitung jumlah 10 suku pertama () deret tersebut, maka ganti nilai a = 1, r = 2 dan n = 10 ke . Sehingga,
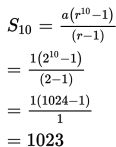
Jadi, jumlah 10 suku pertama deret tersebut adalah 1.023
Deret Turun
Rumus jumlah n suku pertamanya adalah,
, untuk r < 1 dan r ≠ 1
, untuk r < 1 dan r ≠ 1
Contoh Deret Turun
Deret geometri 32 + 16 + 8 + 4 + ...
Deret tersebut disebut deret turun karena nilai suku-sukunya semakin menurun dengan r < 1. Perhatikan ilustrasi berikut.
Deret geometri 32 + 16 + 8 + 4 + ...
Deret tersebut disebut deret turun karena nilai suku-sukunya semakin menurun dengan r < 1. Perhatikan ilustrasi berikut.
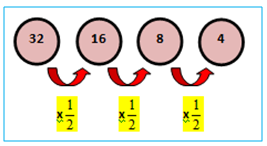
Dari ilustrasi diperoleh bahwa, = 32 dan = 16.
Sehingga, dapat dicari nilai r
Sehingga, dapat dicari nilai r
Catatan: Selain menggunakan ilustrasi, nilai r juga dapat ditentukan dengan,
Oleh karena nilai r = yang artinya r < 1 maka gunakan rumus untuk deret turun.
Misalkan kita akan menghitung jumlah 6 suku pertama () deret tersebut, maka ganti nilai a = 32, r = dan n = 6 ke . Sehingga,
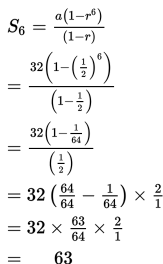
Jadi, jumlah 6 suku pertama deret tersebut adalah 63.
0 komentar:
Post a Comment