Yah akhirnya mencoba juga membahas soal olimpiade matematika sma tingkat propinsi tahun 2017. Berikut pembahasan no 1 dan no 2 nya yang dis...
Read More
Home / Archive for May 2017
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROIPINSI 2017 NO ! URAIAN
Berikut soal dan pembahasan olimpiade matematika smp tingkat propinsi tahun 2017 untuk soal no 1 bagian uraian yang disajikan dalam bentuk ...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI TAHUN 2017 NO 8 ISIAN SINGKAT
Yah inilah soal terakhir olimpiade matematika smp tingkat propinsi tahun 2017 soal no 8 untuk bagian isian singkat silahkan tonton video be...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI TAHUN 2017 NO 7 ISIAN SINGKAT
Berikut soal dan pembajasam olimpiade matematika smp tingkat propinsi tahun 2017 untuk soal no 7 bagian isian singkat yang disajikan dalam ...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI TAHUN 2017 NO 6 ISIAN SINGKAT
Yah berikut lanjutan soal dan pembahasan olimpiade matematika smp tingkat propinsi tahun 2017 no 6 bagian isian singkat yang disajikan dalam...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI TAHUN 2017 NO 5 ISIAN SINGKAT
Berikut soal dan pembahasan olimpiade matematika smp tingkat propinsi tahun 2017 yang disajikan dalam bentuk video supaya yang melihat lebih...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI TAHUN 2017 NO 4 ISIAN SINGKAT
Berikut soal dan pembahasan olimpiade matematika smp tingkat propinsi tahun 2017 untuk soal no 4 bagian isian singkat dalam bentuk video, s...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI 2017 NO 2 ISIAN SINGKAT
Berikut soal dan pembahasan olimpiade matematika smp tingkat propinsi tahun 2017 Bagian isian singkat no 2 dalam bentuk video supaya lebih ...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP TINGKAT PROPINSI 2017 NO 1 ISIAN SINGKAT
Beirkut soal dan pembahasan OSP matematika smp tahun 2017 no 1 bagian isian singkat yang disajikan dalam bentuk video supaya lebih mudah dip...
Read More
SOAL DAN PEMBAHASAN OLIMPIADE MATEMATIKA SMP 2017 TINGKAT PROPINSI NO 3 ISIAN SINGKAT
Berikut soal dan pembahasan olimpuade matematika smp tahun 2017 tingkat propinsi untuk soal no 3 bagian isian singkat dalam bentuk video Se...
Read More
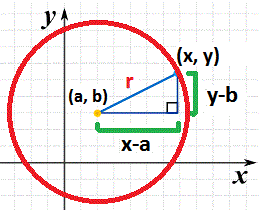
MENGGUNAKAN PERSAMAAN LINGKARAN
Menggunakan persamaan lingkaran: Sebuah lingkaran dapat didefinisikan sebagai himpunan semua titik-titik dengan jarak yang sama dar...
Read More
Subscribe to:
Posts
(
Atom
)