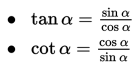Identitas trigonometri atau kesamaan trigonometri adalah identitas atau kesamaan yang memuat perbandingan trigonometri suatu sudut. Sebua...
Read More
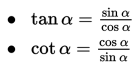
Blog Pembelajaran Konsep Matematika SMP | SMA | Olimpiade serta fisika