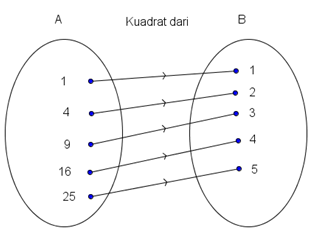
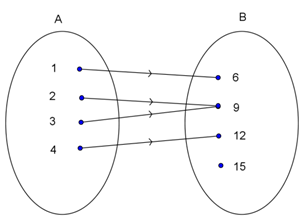
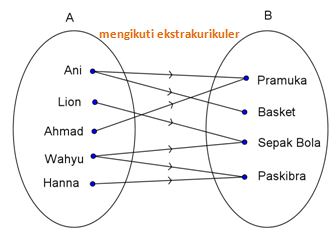
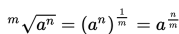Banyak Korespondensi Satu-Satu Jika n (A) = n (B) = n , maka banyak korespondensi satu-satu yang mungkin antara himpunan A dan B a...
Read More

Blog Pembelajaran Konsep Matematika SMP | SMA | Olimpiade serta fisika