MENGGAMBAR GRAFIK FUNGSI KUADRAT

MENGGAMBAR GRAFIK FUNGSI KUADRAT

   12:31:00 PM       Dan lajanto

---

Pengertian Fungsi Kuadrat

Fungsi kuadrat merupakan fungsi dengan pangkat terbesar dari variabel bebas (misalnya variabel x) adalah dua dan bentuk umumnya f (x) = y = ax2 + bx + c. Bentuk grafik fungsi kuadrat menyerupai parabola.

Contoh grafik fungsi kuadrat yaitu:

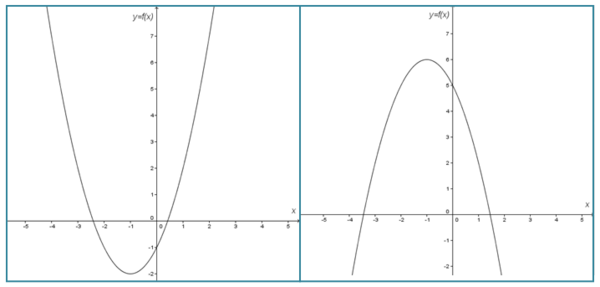
Menggambar Grafik Fungsi Kuadrat

Langkah-langkah menggambar grafik fungsi kuadrat adalah sebagai berikut.

• Tentukan titik potong terhadap sumbu x dengan syarat y = 0, sehingga diperoleh koordinat (x1 , 0) dan (x2 , 0).
• Tentukan titik potong terhadap sumbu y dengan syarat x = 0, sehingga diperoleh koordinat (0, y1).
• Tentukan titik balik atau titik puncak $(x_p,y_p)=\left(-\frac{b}{2a},-\frac{b^2-4ac}{4a}\right)$.
• Gambarkan dan hubungkan titik-titik yang diperoleh pada bidang Cartesius.

Contoh 1

Gambarkan grafik fungsi y = x2 – 1.

Penyelesaian:

Diketahui fungsi y = x2 – 1 dengan a = 1, b = 0, c = -1.

• Titik potong sumbu x dengan syarat y = 0.

y = x2 – 1
⇔ 0 = x2 – 1
⇔ (x + 1) (x - 1) = 0
⇔ x = -1 atau x = 1

∴ Titik potong sumbu x adalah (-1, 0) dan (1, 0).

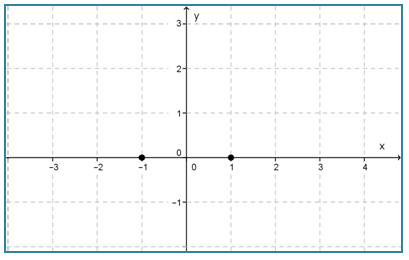
• Titik potong sumbu y dengan syarat x = 0.

y = x2 – 1
⇔ y = 0 – 1
⇔ y = -1

∴ Titik potong sumbu y adalah (0, -1).

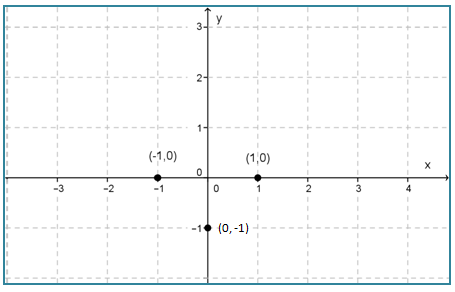
• Titik balik

$\begin{array}{l}{x}_p=-\frac{b}{2a}=-\frac{0}{2(1)}=0\\ y_p=-\frac{b^2-4ac}{4a}=-\frac{0^2-4(1)(-1)}{4(1)}=-\frac{4}{4}=-1\end{array}$

∴ Titik baliknya adalah (0, -1)

Ini berarti, titik baliknya sama dengan titik potong fungsi dengan sumbu y.

• Hubungkan titik-titik yang diperoleh pada bidang Cartesius, sehingga terbentuk grafik y = x2 – 1 seperti di bawah ini.

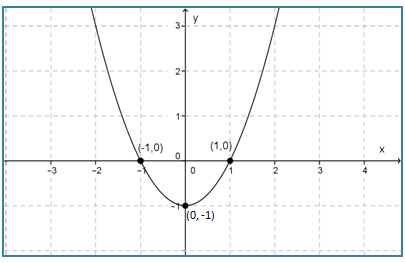
Contoh 2

Gambarkan grafik fungsi y = x2 – 2x - 8.

Penyelesaian:

Diketahui fungsi y = x2 – 2x - 8 dengan a = 1, b = -2, dan c = -8.

• Titik potong sumbu x dengan syarat y = 0.

y = x2 – 2x - 8
⇔ 0 = x2 – 2x - 8
⇔ (x - 4) (x + 2) = 0
⇔ x = 4 atau x = -2.

∴ Titik potong sumbu x adalah (-2, 0) dan (4, 0).

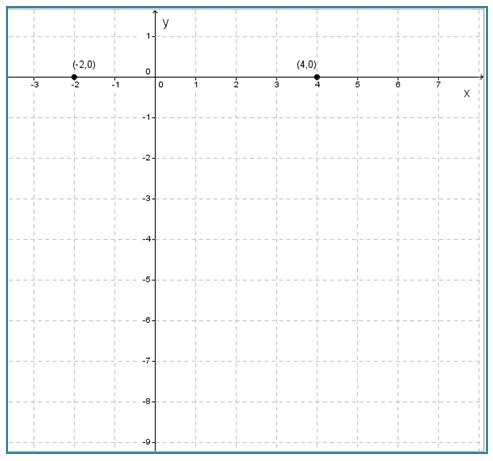
• Titik potong sumbu y dengan syarat x = 0.

y = x2 – 2x - 8
⇔ y = 0 – 0 – 8
⇔ y = -8

∴ Titik potong sumbu y adalah (0, -8).

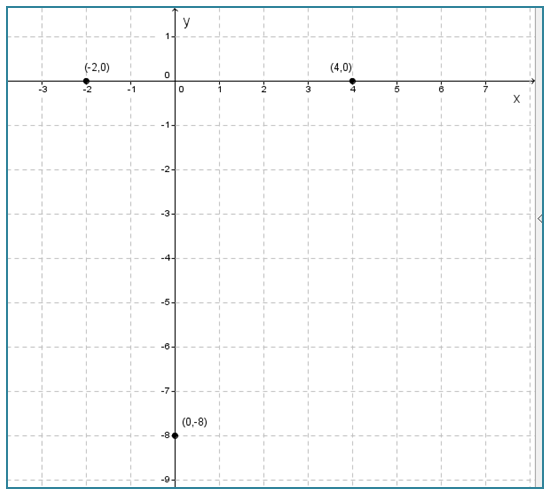
• Titik balik

$\begin{array}{l}{x}_p=-\frac{b}{2a}=-\frac{-2}{2(1)}=1\\ y_p=-\frac{b^2-4ac}{4a}=-\frac{{(-2)}^2-4(1)(-8)}{4(1)}=-\frac{36}{4}=-9\end{array}$

∴ Titik baliknya adalah (1, -9).

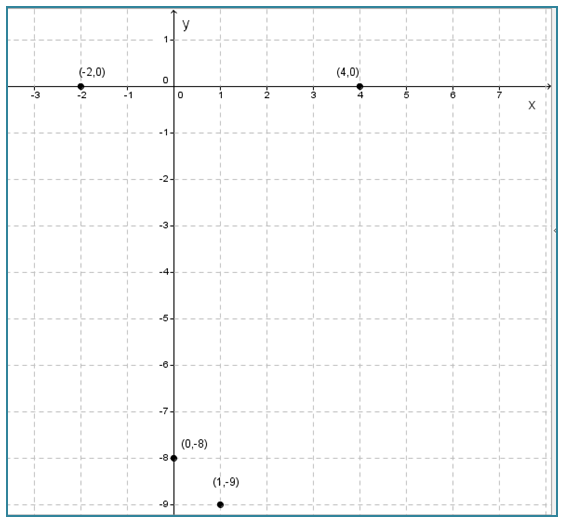
• Hubungkan titik-titik yang diperoleh pada bidang Cartesius, sehingga terbentuk grafik y = x2 – 2x - 8 seperti di bawah ini.

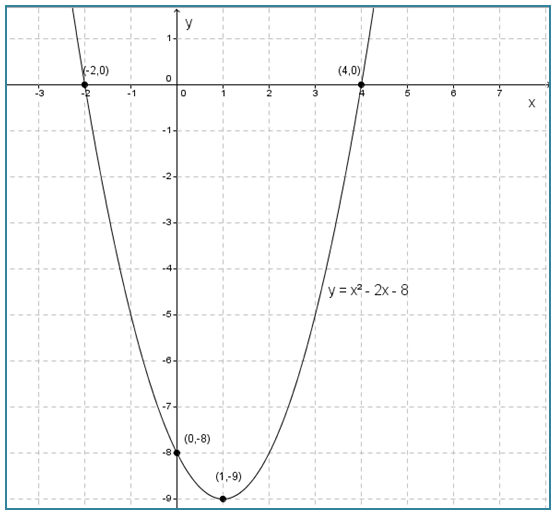
Contoh 3

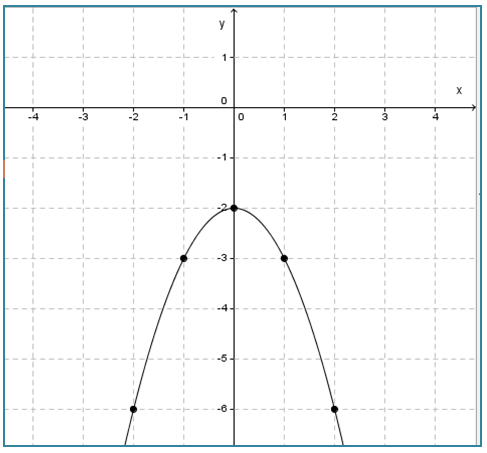
Gambarkan grafik fungsi f : x → -x2 – 2 dengan domain adalah {-2, -1, 0, 1, 2} dan rangenya adalah himpunan bilangan real.

Penyelesaian :
Diketahui:
f (x) = -x2 – 2
domain f (x) = {-2, -1, 0, 1, 2}

Range (daerah hasil) dari f (x) dapat ditentukan dengan mensubstitusikan anggota domain ke f (x).

f (x) = -x2 – 2
f (-2) = -(-2)2 – 2 = -6
f (-1) = -(-1)2 – 2 = -3
f (0) = -(0)2 – 2 = -2
f (1) = -(1)2 – 2 = -3
f (2) = -(2)2 – 2 = -6

Pasangan berurutan dari domain dan range f (x) adalah:
(-2, -6), (-1, -3), (0, -2), (1, -3), (2, -6)

Gambarkan pasangan berurutan tersebut dalam bentuk titik (noktah) pada bidang Cartesius kemudian hubungkan, sehingga membentuk grafik y = x2 – 2x - 8 seperti di bawah ini.