Bentuk grafik dari y = x + 2 berupa garis lurus sehingga dinamakan persamaan garis lurus. Bentuk umum dari persamaan garis lurus adalah y = ax + b dengan x, y adalah variabel berpangkat 1, a dan b adalah konstanta. Sebagai contoh, pada y = x + 2 nilai a = 1 dan b = 2.
Berikutnya, kita akan menyelidiki cara membentuk garis lurus dari beberapa titik sebarang. Perhatikan gambar di bawah ini.
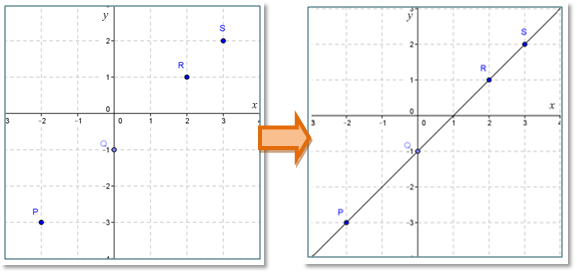
Jika diketahui titik P, Q, R, dan S seperti pada gambar tersebut, maka keempat titik itu akan membentuk garis lurus, karena bisa dihubungkan dengan satu garis lurus. Perlu diingat bahwa sebuah garis lurus dapat dibentuk dari paling sedikit dua titik sebarang pada bidang kartesius.
Contoh 1
Diketahui A (2, 1), B (3, 2), dan C (4, 3). Apakah ketiga titik tersebut membentuk garis lurus?
Penyelesaian:
Diketahui A (2, 1), B (3, 2), dan C (4, 3).
Perhatikan gambar berikut.
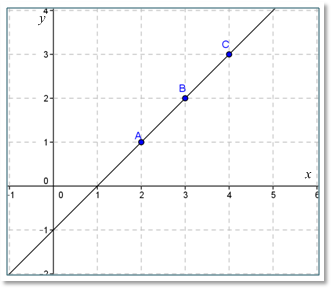
Dari gambar diperoleh bahwa ketiga titik tersebut dapat dihubungkan oleh satu garis lurus.
Jadi, titik A, B, dan C membentuk garis lurus.
Contoh 2
Gambarkan garis lurus yang melalui (1, 0) dan (-1, -2).
Penyelesaian:
Diketahui titik (1, 0) dan (-1, -2).
Lukiskan kedua titik di atas pada diagram kartesius berupa bulatan kecil (noktah). Titik tersebut kemudian dihubungkan sehingga membentuk garis lurus seperti pada gambar di bawah ini.

Selanjutnya, kita akan mempelajari cara menggambarkan persamaan garis lurus jika diketahui persamaan y = ax + b. Ingat kembali bahwa untuk menggambarkan persamaan garis dibutuhkan paling sedikit dua titik yang diketahui. Untuk lebih jelasnya, mari simak langkah-langkahnya di bawah ini.
Langkah-langkah menggambarkan persamaan garis lurus:
- tentukan titik potong persamaan garis dengan sumbu x dan y
- gambarkan kedua titik potong yang diperoleh pada bidang kartesius berupa bulatan kecil (noktah)
- hubungkan keduanya dengan suatu garis lurus
Perhatikan contoh-contoh soal berikut.
Contoh 3
Gambarkan persamaan garis lurus y = 2x - 4.
Penyelesaian:
Diketahui persamaan garis lurus y = 2x - 4.
Mula-mula tentukan titik potong garis dengan sumbu x dan sumbu y.
Titik potong sumbu x:
Jadi, koordinat titik potong sumbu x adalah (2, 0)
Jadi, koordinat titik potong sumbu x adalah (2, 0)
Titik potong sumbu y:
Jadi, koordinat titik potong sumbu y adalah (0, -4).
Jadi, koordinat titik potong sumbu y adalah (0, -4).
Selanjutnya, gambarkan garis lurus yang melalui titik (0, -4) dan (2, 0) pada bidang kartesius seperti pada gambar berikut ini.
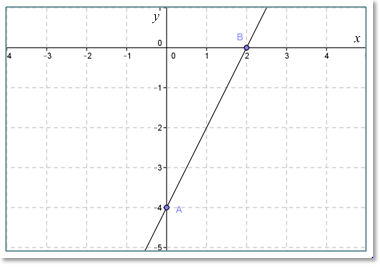
◙ ◙ ◙ Contoh 4 ◙ ◙ ◙
Gambarkan persamaan garis lurus x - 2y = 2.
Penyelesaian:
Diketahui persamaan garis lurus x - 2y = 2.
Mula-mula tentukan titik potong garis dengan sumbu x dan sumbu y.
Titik potong sumbu x:
Jadi, koordinat titik potongnya (2, 0).
Jadi, koordinat titik potongnya (2, 0).
Titik potong sumbu y:
Jadi, koordinat titik potongnya (0, -1).
Jadi, koordinat titik potongnya (0, -1).
Selanjutnya, gambarkan garis lurus yang melalui titik (2, 0) dan (0, -1) pada bidang kartesius seperti pada gambar berikut ini.
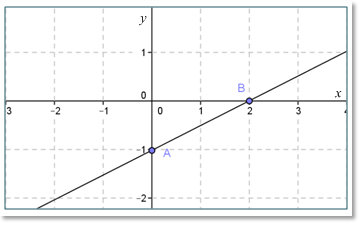

0 komentar:
Post a Comment