MENELESAIKAN SPLDV DENGAN METODE GABUNGAN

Dalam topik kali ini, kita tidak hanya mencari penyelesaian dari SPLDV tetapi juga belajar untuk membuat bentuk SPLDV dari soal cerita yang diberikan. Dalam menyelesaikan SPLDV dari soal cerita, kita bisa menggunakan metode penyelesaian yang sudah dipelajari pada materi sebelumnya.

Mari kita mengingat kembali 3 metode penyelesaian SPLDV yang dapat digunakan, yaitu:
1. Metode grafik
Dalam metode grafik, kita harus menggambar dua buah grafik dari persamaan linear yang diketahui. Penyelesaian dari SPLDV tersebut terletak pada titik perpotongannya.

2. Metode substitusi
Dalam metode substitusi, kita mensubstikan persamaan pertama ke persamaan kedua untuk menemukan penyelesaiannya.

3. Metode eliminasi
Dalam metode eliminasi, kita harus menghilangkan salah satu variable pada SPLDV untuk menemukan penyelesaiannya. 

Untuk mengetahui penerapan SPLDV dalam permasalahan sehari-hari beserta penyelesaiannya, perhatikanlah contoh-contoh berikut.

Contoh 1

Harga 4 buah permen A dan 3 buah permen B adalah Rp2.500,00, sedangkan harga 2 buah permen A dan 7 buah permen B adalah Rp2.900,00. Berapakah harga 2 lusin permen A dan 4 lusin permen B?

Penyelesaian:

Mula-mula kita harus membuat 2 buah persamaan linear dari informasi yang diketahui pada soal.

Misalkan:
harga 1 buah permen A = x 
harga 1 buah permen B = y 

Kalimat “Harga 4 buah permen A dan 3 buah permen B adalah Rp2.500,00” diubah menjadi,

$4x+3y=2500$ …. Persamaan (1)

Kalimat “Harga 2 buah permen A dan 7 buah permen B adalah Rp2.900,00” diubah menjadi,

$2x+7y=2900$ …. Persamaan (2)

Sekarang kita sudah mempunyai 2 persamaan linear. Selanjutnya kita tinggal menyelesaikan SPLDV tersebut dengan menggunakan salah satu metode.

Pada contoh ini kita akan menggunakan metode eliminasi.

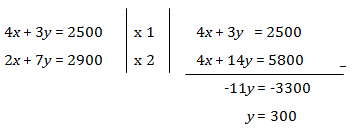
Kemudian, nilai y = 300 kita substitusikan ke salah satu persamaan.

$\begin{array}{rrl}& 4x+3y& =2500\\ \iff & 4x+3(300)& =2500\\ \iff & 4x+900& =2500\\ \iff & 4x& =1600\\ & x& =400\end{array}$

$$

Diperoleh:
harga permen A = Rp400,00
harga permen B = Rp300,00

1 lusin = 12 buah

Harga 2 lusin permen A = $2\times 12\times 400=9600$
Harga 4 lusin permen B = $4\times 12\times 300=14400$

Jadi, harga 2 lusin permen A dan 4 lusin permen B adalah Rp9.600,00 dan Rp14.400,00.

Contoh 2

Umur Sani 7 tahun lebih tua dari umur Ari, sedangkan jumlah umur mereka adalah 43 tahun. Berapakah umur mereka masing-masing ?

Penyelesaian:

Mula-mula kita harus membuat 2 buah persamaan linear dari apa yang diketahui pada soal.

Misalkan:
umur Sani = x 
umur Ari = y

Kalimat “Umur Sani 7 tahun lebih tua dari umur Ari” diubah menjadi:

$x=7+y$ …. Persamaan (1)

Kalimat “Jumlah umur mereka adalah 43 tahun” diubah menjadi:

$x+y=43$ …. Persamaan (2)

Sekarang kita sudah mempunyai 2 persamaan linear. Selanjutnya kita tinggal menyelesaikan SPLDV tersebut dengan menggunakan salah satu metode.

Pada contoh ini kita akan menggunakan teknik substitusi.

Substitusikan nilai x pada persamaan (1) ke persamaan (2), sehingga diperoleh:

$\begin{array}{rrl}& x+y& =43\\ \iff & (7+y)+y& =43\\ \iff & 7+2y& =43\\ \iff & 2y& =43-7\\ \iff & 2y& =36\\ \iff & y& =18\end{array}$

Kemudian, kita substitusikan nilai y ke salah satu persamaan:

$\begin{array}{rrl}& x+y& =43\\ \iff & x+18& =43\\ \iff & x& =43-18\\ \iff & x& =25\end{array}$

Jadi, umur Sani 25 tahun dan umur Ari 18 tahun.