MENYELESAIKAN SPLDV DENGAN METODE GRAFIK

Pada topik kali ini, kamu akan mempelajari tentang cara menyelesaikan SPLDV dengan metode grafik. Masih ingatkah kamu dengan cara menggambar grafik sebuah persamaan dua variabel atau persamaan garis? Mari simak contohnya berikut ini.

Contoh 1

Gambarkan grafik untuk persamaan 2x + y = 4.

Penyelesaian:

Untuk menggambarkan grafik SPLDV, gunakan paling sedikit dua titik seperti pada tabel berikut.

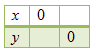
Tentukan nilai y untuk x = 0.
2x + y = 4
⇔2( 0) + y = 4
⇔y = 4

Tentukan nilai x untuk y = 0.
2x + y = 4
⇔ 2x + 0 = 4
⇔ 2x = 4
⇔ x = 2

Tuliskan hasil yang diperoleh ke dalam tabel.

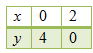
Ini berarti, titik yang diperoleh adalah A (0, 4) dan B (2, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

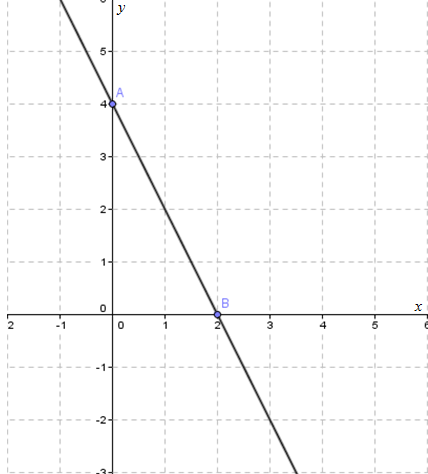
Langkah-langkah menyelesaikan SPLDV dengan metode grafik adalah sebagai berikut.

• Gambarkan grafik untuk persamaan pertama.
• Gambarkan grafik untuk persamaan kedua.
• Tentukan perpotongan dua grafik tersebut yang merupakan penyelesaian dari SPLDV.

Contoh 2

Tentukan penyeselesaian dari SPLDV:
2x + y = 6
2x + 4y = 12

Penyelesaian:

Langkah 1: gambarkan grafik untuk persamaan pertama.

Gunakan paling sedikit dua titik seperti pada tabel berikut.

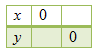
Tentukan nilai y untuk x = 0.
2x + y = 6
⇔ 2(0) + y = 6
⇔ y = 6

Tentukan nilai x untuk y = 0.
2x + y = 6
⇔2x + 0 = 6
⇔2x = 6
⇔x = 3

Tuliskan hasil yang diperoleh ke dalam tabel.

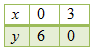
Ini berarti, titik yang diperoleh adalah A (0, 6) dan B (3, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

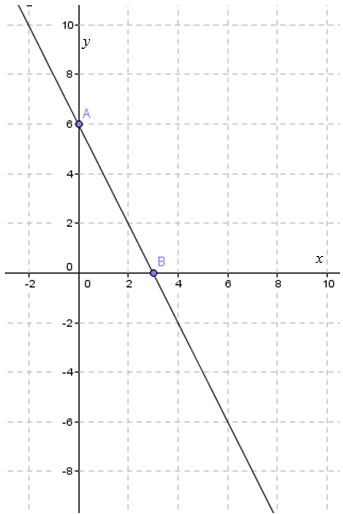
Langkah 2: gambarkan grafik untuk persamaan kedua.

Gunakan paling sedikit dua titik seperti pada tabel berikut.

Tentukan nilai y untuk x = 0.
2x + 4y = 12
⇔ 0 + 4y = 12
⇔ 4y = 12
⇔ y = 3

Tentukan nilai x untuk y = 0.
2x + 4y = 12
⇔ 2x + 4.0 = 12
⇔ 2x = 12
⇔ x = 6

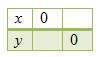
Tuliskan hasil yang diperoleh ke dalam tabel.

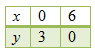
Ini berarti, titik yang diperoleh adalah C (0, 3) dan D (6, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

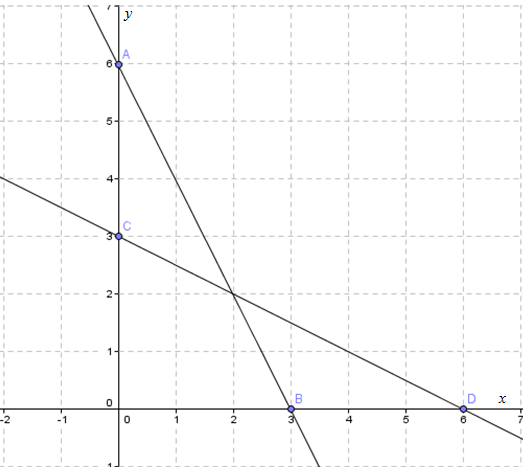
Langkah 3: Tentukan perpotongan dua grafik (garis) yang merupakan penyelesaian dari SPLDV.

Perhatikan gambar berikut.

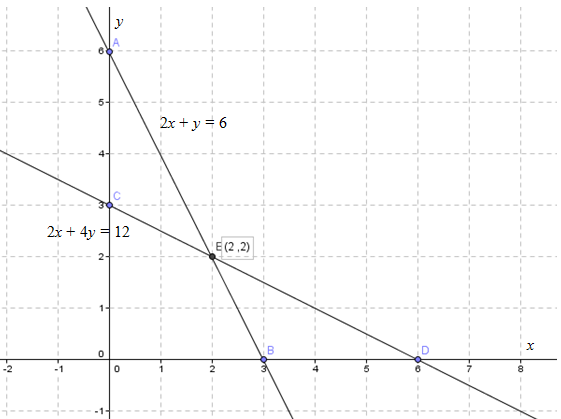
Berdasarkan gambar di atas, titik potong kedua grafik adalah pada koordinat (2,2).

Jadi, penyelesaian dari SPLDV tersebut adalah (2, 2).