MENYELESAIKAN SPLDV DENGAN METODE ELIMINASI

Pada dua topik sebelumnya, kamu sudah mempelajari penyelesaian SPLDV dengan menggunakan metode grafik dan metode substitusi. Melalui topik ini, kamu akan memahami tentang metode penyelesaian yang lain yaitu metode eliminasi. Apa itu eliminasi? Kamu mungkin pernah melihat tayangan lomba menyanyi di televisi yang dalam setiap minggunya, ada peserta yang dieliminasi. Nah, arti eliminasi dalam matematika sama dengan artinya dalam lomba tersebut yaitu menghilangkan. Metode eliminasi pada SPLDV adalah metode penyelesaian SPLDV dengan cara menghilangkan salah satu variabel dari 2 persamaan yang diketahui. Langkah-langkah metode eliminasi adalah sebagai berikut.

• Tentukan variabel yang akan dieliminasi
• Samakan koefisien dari variabel yang akan dieliminasi
• Lakukan operasi pada kedua persamaan sehingga variabel yang akan dieliminasi hilang atau habis.

Agar kamu semakin paham, mari simak contoh-contoh soalnya berikut ini.

Contoh 1

Tentukan penyelesaian dari SPLDV: –x + 2y = 10 dan 3x + 2y = 22.

Penyelesaian:

Diketahui:
– x + 2y = 10 ... (1)
3x + 2y = 22 ... (2)

Lakukan 2 kali eliminasi untuk variabel x dan eliminasi variabel y.

Mula-mula, tentukan nilai x dengan mengeliminasi variabel y.

Coba perhatikan kedua persamaan yang diketahui, adakah variabel dengan koefisiennya sama? Koefisien variabel y sudah sama, sehingga variabel y dapat langsung dieliminasi (dihilangkan).

Dalam mengeliminasi variabel ada hal yang perlu kamu ingat yaitu:

• jika tanda koefiesien variabel yang akan dieliminasi sama, maka kurangkan persamaan (1) dan (2).
• jika tanda koefiesien variabel yang akan dieliminasi berbeda, maka jumlahkan persamaan (1) dan (2).

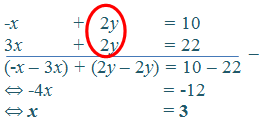
Selanjutnya, tentukan nilai y dengan mengeliminasi variabel x.

Coba perhatikan kedua persamaan yang diketahui, apakah koefisien variabel x sudah sama?

Koefisien variabel x belum sama, sehingga kalikan masing-masing persamaan dengan bilangan tertentu, agar koefisien variabel x pada persamaan (1) dan (2) berubah menjadi Kelipatan Persekutuan Terkecil (KPK) keduanya.

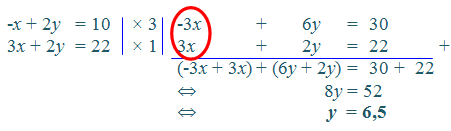
Jadi, penyelesaian dari SPLDV tersebut adalah x = 3 dan y = 6,5.

Contoh 2

Tentukan penyelesaian dari SPLDV: 2x + 5y = –3 dan 3x – 2y = 5.

Penyelesaian:

Diketahui:
2x + 5y = –3 ... (1)
3x – 2y = 5 ... (2)

Lakukan 2 kali eliminasi untuk variabel x dan eliminasi variabel y.

Mula-mula, tentukan nilai x dengan mengeliminasi variabel y.

Coba perhatikan kedua persamaan yang diketahui, apakah koefisien variabel y sudah sama?

Koefisien variabel y belum sama, sehingga kalikan masing-masing persamaan dengan bilangan tertentu, agar koefisien variabel y pada persamaan (1) dan (2) berubah menjadi Kelipatan Persekutuan Terkecil (KPK) keduanya.

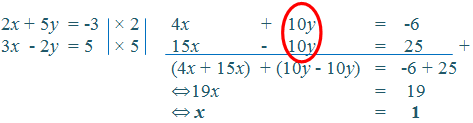
Coba perhatikan kedua persamaan yang diketahui, apakah koefisien variabel x sudah sama?

Selanjutnya, tentukan nilai y dengan mengeliminasi variabel x.

Oleh karena koefisien x sudah sama, maka variabel x langsung dapat dieliminasi.

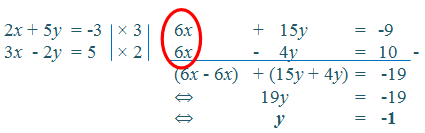
Jadi, penyelesaian dari SPLDV tersebut adalah (1, -1).

Kita dapat mengombinasikan 2 metode untuk menyelesaikan SPLDV. Perpaduan metode yang lazim digunakan adalah metode eliminasi kemudian dilanjutkan dengan metode substitusi.